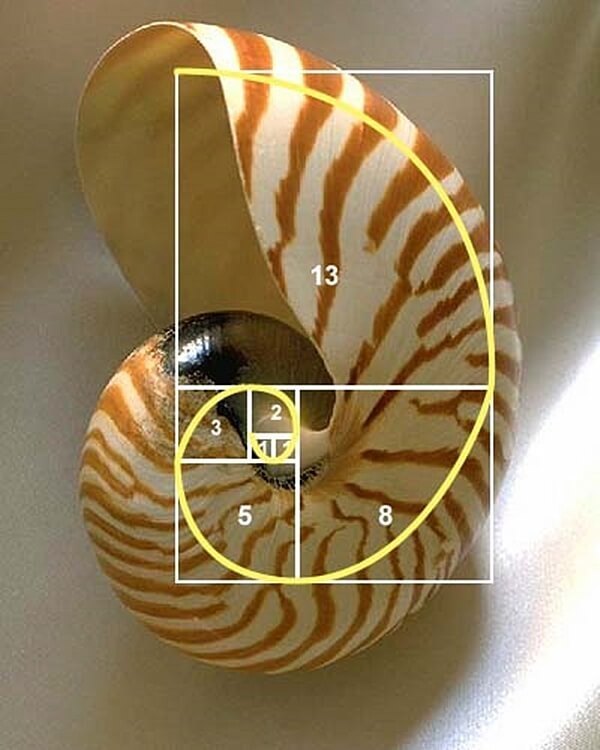
Спираль Фибоначчи: почерк Творца, который вы можете увидеть в совершенно разных объектах природы (видео)





Существует порядок в природе и гармония во Вселенной, которая не может быть очевидной. То, что изначально выглядит продуктом полного хаоса — ураган или сотни семян подсолнечника, — на самом деле аккуратно вписывается в математическую формулу — последовательность Фибоначчи.
Формула
Последовательность Фибоначчи – это числовая схема, в которой следующее число в последовательности образуется путем сложения двух предыдущих чисел вместе: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, и т. д.
В мире природы она присутствует в лепестках или листьях многих растений, в строении ананасов и артишоков, в раковине наутилуса, а также в галактиках в космосе и в ураганах над океаном.
Числа Фибоначчи также используются в информатике и финансах для определения интервала, когда цена актива перестанет подниматься и начнет терять значение.
Ведущий математик Средневековья
Последовательность Фибоначчи носит имя Леонардо Пизано Биголло, родившегося в конце XII века в Республике Пиза. Он также был известен как Леонардо Пизанский или по прозвищу Фибоначчи, что переводится как «сын Боначчи». Его отец был торговцем, который был назначен для оказания помощи группе торговцев-пизан, работающих в портах Северной Африки. Там Фибоначчи учился у мастера-математика. Он также много путешествовал, посетив Египет, Грецию, Сицилию и Сирию, где продолжал изучение математики.
Фибоначчи признан одним из ведущих математиков Средневековья. Он был приглашен предстать перед императором Священной Римской империи Фридрихом II. Считается, что числовой шаблон Фибоначчи был впервые идентифицирован в Древней Индии и использовался там при изучении поэтического размера.
Божественный замысел
Последовательность Фибоначчи можно использовать для моделирования или описания удивительного множества явлений в математике и науке, искусстве и природе. Но никто не может объяснить, почему они так ясно отражены в мире искусства и природы.
Последовательность Фибоначчи, также называемаясерией Фибоначчи, является системой нумерации природы. Нихат Парвейн, биохимик из Университета Джорджии, говорит, что этот математический порядок скрыт в «кажущейся случайности» природного мира. «Числа Фибоначчи появляются повсюду в природе, от расположения листьев в растениях до рисунка лепестков цветка, прицветников соснового конуса или чешуи ананаса, — пишет она. — Эти числа применимы к росту каждого живого существа, включая одну клетку, пшеничное зерно, улей пчел и даже все человечество».
Серия Фибоначчи проявляется в трех лепестках лилии, в то время как лютики имеют пять лепестков, а некоторые ромашки — 21 или 34. Это все числа Фибоначчи. Порядок также соблюдается в плодах бананов (три секции) и яблок (пять секций), в способе расположения ветвей на дереве и листьев на каждой ветке.
В животном мире последовательность Фибоначчи наблюдается у улиток и в камерной раковине наутилуса, которая представляет собой логарифмическую спираль, или у морской звезды с ее пятью вершинами.
Галактики, такие как Млечный Путь, имеют спиральные рукава, которые следуют шаблону Фибоначчи, как и ураганы. Их форма удивительно похожа на форму наутилуса.
«Повсеместное распространение и поразительная функциональность в природе предполагают важность последовательности Фибоначчи как фундаментальной характеристики Вселенной», — пишет Джордж Дворский, канадский биоэтик и футурист.
Источник
СПИРАЛЬ ФИБОНАЧЧИ — зашифрованный закон природы
Числа Фибоначчи — числовая последовательность, где каждый последующий член ряда равен сумме двух предыдущих, то есть: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368. 75025. 3478759200, 5628750625. 260993908980000. 422297015649625. 19581068021641812000. Изучением сложных и удивительных свойств чисел ряда Фибоначчи занимались самые различные профессиональные ученые и любители математики.
В 1997 году несколько странных особенностей ряда описал исследователь Владимир Михайлов, который был убежден, что Природа (в том числе и Человек) развивается по законам, которые заложены в этой числовой последовательности.
Замечательным свойством числового ряда Фибоначчи является то, что по мере увеличения чисел ряда отношение двух соседних членов этого ряда асимптотически приближается к точной пропорции Золотого сечения (1:1,618) — основе красоты и гармонии в окружающей нас природе, в том числе и в человеческих отношениях.
Отметим, что сам Фибоначчи открыл свой знаменитый ряд, размышляя над задачей о количестве кроликов, которые в течении одного года должны родиться от одной пары. У него получилось, что в каждом последующем месяце после второго число пар кроликов в точности следует цифровому ряду, которое ныне носит его имя. Поэтому не случайно, что и сам человек устроен по ряду Фибоначчи. Каждый орган устроен в соответствии с внутренней, или внешней двойственностью.
Числа Фибоначчи привлекли математиков своей особенностью возникать в самых неожиданных местах. Замечено, например, что отношения чисел Фибоначчи, взятых через одно, соответствуют углу между соседними листьями на стебле растений, точнее, они говорят, какую долю оборота составляет этот угол: 1/2 — для вяза и липы, 1/3 — для бука, 2/5 — для дуба и яблони, 3/8 — для тополя и розы, 5/13 — для ивы и миндаля и т. д. Эти же числа вы найдете при подсчете семян в спиралях подсолнуха, в количестве лучей, отражающихся от двух зеркал, в количестве вариантов маршрутов переползания пчелы от одной соты к другой, во многих математических играх и фокусах.
В чем разница между спиралями золотого сечения и спиралью Фибоначчи? Спираль золотого сечения идеальна. Она соответствует Первоисточнику гармонии. Эта спираль не имеет ни начала, ни конца. Она бесконечна. Спираль Фибоначчи имеет начало, от которого она начинает “раскрутку”. Это очень важное свойство. Оно позволяет Природе после очередного замкнутого цикла осуществлять строительство новой спирали с “нуля”.
Следует сказать, что спираль Фибоначчи может быть двойной. Существуют многочисленные примеры этих двойных спиралей, встречающихся повсюду. Так, спирали подсолнухов всегда соотносятся с рядом Фибоначчи. Даже в обычной сосновой шишке можно увидеть эту двойную спираль Фибоначчи. Первая спираль идет в одну сторону, вторая — в другую. Если посчитать число чешуек в спирали, вращающейся в одном направлении, и число чешуек в другой спирали, можно увидеть, что это всегда два последовательных числа ряда Фибоначчи. Число этих спиралей 8 и 13. В подсолнухах встречаются пары спиралей: 13 и 21, 21 и 34, 34 и 55, 55 и 89. И отклонений от этих пар не бывает.
У Человека в наборе хромосом соматической клетки (их 23 пары) источником наследственных болезней являются 8, 13 и 21 пары хромосом.
Но почему в Природе именно этот ряд играет решающую роль? На этот вопрос может дать исчерпывающий ответ концепция тройственности, определяющая условия ее самосохранения. При нарушении «баланса интересов» триады одним из ее «партнеров», «мнения» двух других «партнеров» должны быть скорректированы. Особенно наглядно концепция тройственности проявляется в физике, где из кварков построили «почти» все элементарные частицы. Если вспомнить, что отношения дробных зарядов кварковых частиц составляют ряд , а это и есть первые члены ряда Фибоначчи, которые необходимы для формирования других элементарных частиц.
Возможно, что спираль Фибоначчи может играть решающую роль и в формировании закономерности ограниченности и замкнутости иерархических пространств. Действительно, представим, что на каком-то этапе эволюции спираль Фибоначчи достигла совершенства (она стала неотличима от спирали золотого сечения) и по этой причине частица должна трансформироваться в следующую «категорию».
Эти факты еще раз подтверждают, что закон о двойственности дает не только качественные, но и количественные результаты. Они заставляют задуматься о том, что окружающий нас Макромир и Микромир эволюцирует по одним и тем же законам — законам иерархии, и что эти законы едины для живой и для неживой материи.
Все это свидетельствует о том, что ряд чисел Фибоначчи представляет собой некий зашифрованный закон природы.
Цифровой код развития цивилизации можно определить с помощью различных методов в нумерологии. Например, с помощью приведения сложных чисел к однозначным (например, 15 есть 1+5=6 и т.д.). Проводя подобную процедуру сложения со всеми сложными числами ряда Фибоначчи, Михайлов получил следующий ряд этих чисел: 1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 8, 1, 9, затем все повторяется 1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 4, 8, 8. и повторяется вновь и вновь. Этот ряд также обладает свойствами ряда Фибоначчи, каждый бесконечно последующий член равен сумме предыдущих. Например, сумма 13-го и 14-го членов равна 15, т.е. 8 и 8=16, 16=1+6=7. Оказывается, что этот ряд периодичный, с периодом в 24 члена, после чего, весь порядок цифр повторяется. Получив этот период, Михайлов выдвинул интересное предположение — не является ли набор из 24 цифр своеобразным цифровым кодом развития цивилизации?опубликовано econet.ru
P.S. И помните, всего лишь изменяя свое сознание — мы вместе изменяем мир! © econet
Понравилась статья? Напишите свое мнение в комментариях.
Подпишитесь на наш ФБ:
Источник
Последовательность Фибоначчи в природе и живом – спираль и другие проявления золотого сечения
Оглавление. Жми для простмотра
Получаемые математиками закономерности и зависимости часто впоследствии обнаруживаются и в других окружающих явлениях. Таким образом подтверждается высокая степень соответствия математического аппарата для описания природных процессов. Один из примеров такой зависимости – числа Фибоначчи, в природе встречающиеся в самых различных масштабах.
p, blockquote 1,0,0,0,0 —>
p, blockquote 2,0,0,0,0 —>
Лучший брокер
p, blockquote 3,0,0,0,0 —>
Наблюдая за окружающим миром, нельзя не заметить, какое несметное количество листьев колышет ветер на растениях. При взгляде издалека может показаться, что последовательность их расположения совершенно хаотична, абсолютно произвольна. Но в действительности в каждом растении произрастание каждого листика и каждой ветки ясно угадывается та точность, какая может быть присуща только математике.
p, blockquote 4,0,0,0,0 —>
Появившись на свет, оно тут же начинает развиваться строго в соответствии с этим законом, согласно которому на нём не будет ни одного лишнего листка или цветка. Количество веток на новом дереве и где именно они отрастут, количество листьев на каждой из веток и порядок их расположения — всё это заранее записано в генетическом коде растения ещё на стадии его зарождения. Работая вместе, учёные из областей биологии и точных наук открыли миру невероятные законы развития природы — закономерность расположения листьев, известная как филлотаксис, число оборотов вокруг стебля и количество листков в нём происходит в соответствии с последовательностью Фибоначчи, то есть ясно угадывается закон золотого сечения.
p, blockquote 5,0,0,0,0 —>
Если искушённый исследователь желает найти подобные закономерности в биологическом мире, то пусть увидит, как часто они угадываются во всевозможных спиралевидных формах, широко распространённых в царстве растений. Листья обычно прикреплены к стеблю по спирали, идущей между двумя листками: 1/3 от оборота у орешника, например.
p, blockquote 6,0,1,0,0 —>
Ряд Фибоначчи также угадывается в законе симметричной формы цветов и количестве лепестков, как, например, у ириса (3 лепестка) или у златоцвета (8 лепестков).
p, blockquote 7,0,0,0,0 —>
Число, примерно идентичное числу фи, можно обнаружить в соотношениях частей тела у людей. На этом основании облик человека являет собой идеал пропорций, отражаемый отношением: M/m=1,618.
p, blockquote 8,0,0,0,0 —>
Последовательность чисел Фибоначчи в живой природе и ее проявления в жизни
Рассматривая в качестве центра тела расположение его пупка, а длину от нее до ступни –за единичный отрезок, то пропорция человеческого роста составит примерно 1,618.
p, blockquote 9,0,0,0,0 —>
Человек обладает 2-мя руками и 10-ю пальцами на них, состоящих из 3-х фаланг (без учёта большого пальца). Если не принимать в расчёт пальцы с двумя фалангами, то под закон золотого сечения подпадают восемь пальцев. Так получается последовательность Фибоначчи: 2, 3, 5, 8.
p, blockquote 10,0,0,0,0 —>
Закон Фибоначчи в природе человеческих лёгких
В результате специального исследования, проведённого учёными Б.Д. Уэстом и А.Л. Гольдбергером, было обнаружено – общее устройство лёгких человека формируется по золотому сечению. Бронхи, являющиеся неотъемлемой частью человеческих лёгких, отличаются асимметричностью, и заключается это в том, что левый дыхательный путь длиньше, чем правый. Подобная асимметрия характерна и для их всевозможных продолжения, в каждом наиболее мягком дыхательном пути, но отношение длин коротких и длинных бронхов при этом составляет 1:1,618.
p, blockquote 11,0,0,0,0 —>
Многие люди творческих профессий, чья работа связана с изобразительным искусством, составляют свои предварительные зарисовки, применяя мерки с идеального по своей природе человеческого тела. Художники Возрождения творили свои шедевры, заранее взяв мерки геометрических отношений тела, полностью соответствующими золотому числу. Также эти соотношения применялись криминалистами и археологами с целью восстановления по фрагментам тела его полного облика.
p, blockquote 12,0,0,0,0 —>
Ряд Фибоначчи в природе молекулы ДНК
Она вмещает в себя все самые подробные данные о физиологическом строении живого существа. Это касается флоры и фауны. При этом ДНК в своём строении придерживается золотого сечения. Внешне она представляет конструкцию из двух переплетённых спиралей. Длина их равна 34 ангстремам, а ширина – 21.
p, blockquote 13,1,0,0,0 —> 
Удивительно здесь то, что 21 и 24 идут подряд в Фибо-последовательности. Отношение размеров получающейся логарифмической спирали, которую представляет собой молекула ДНК, есть 1:1,618.
p, blockquote 14,0,0,0,0 —>
Спираль Фибоначчи – загадка природы (фото)
Математические науки не знают второй формы, способной сравниться своими свойствами со спиралью, получившей свои оригинальные свойства благодаря положенному в базис структуры Золотое сечение. Напомним, что формула имеет следующий вид: ( a + b )/ a = a / b.
p, blockquote 15,0,0,0,0 —>
Известный золотой прямоугольник приобрёл своё название именно в честь того, что он обладает как раз таким соотношением сторон — отношение его длинных сторон к меньшим равно 1,168:1.
p, blockquote 16,0,0,0,0 —> 
Одним из необыкновенных свойств золотого прямоугольника является то, что если от такой фигуры отделить квадрат, с большей стороной равной длине малой стороны прямоугольника, в результате будет получен ещё один золотой прямоугольник, но меньший по площади.
p, blockquote 17,0,0,0,0 —>
Обычно спиральную структуру наблюдают в закономерности позиций семян подсолнечника, структуре лепестков некоторых видов цветов, в необычной геометрии ракушек.
p, blockquote 18,0,0,0,0 —>
У подавляющего большинства улиток раковина обладает именно спиралевидной формой. Поскольку эти существа не обладают разумом, они не могут владеть элементарными математическими знаниями, достаточными для создания собственной раковины подобной формы. Многие учёные не могут точно определить причину, по которой эти моллюски сумели выбрать такую необычную форму существования.
p, blockquote 19,0,0,1,0 —>
Ясно здесь только, что подобное развитие не может считаться случайным стечением обстоятельств, и сама по себе подобная гипотеза будет выглядеть глупо. Это явно осознанное творение.
p, blockquote 20,0,0,0,0 —>
Спирали также можно найти на ладонях и пальцах человека, элементарно сняв отпечатки.
p, blockquote 21,0,0,0,0 —>
В животном мире встретить огромное количество спиралевидных форм можно буквально повсюду — закрученные рога и бивни некоторых видов животных, когти и клювы некоторых видов птиц.
p, blockquote 22,0,0,0,0 —>
В волнах, закручивающихся на морской или океанской глади, ясно виден математический график золотого сечения Фибоначчи в природе со значениями 1, 1, 2, 3, 5, 8, 13, 21, 34 и 55. Не стоит так же забывать о водоворотах, или, по крайней мере, о воде, сливающейся в раковине в водосточную трубу.
p, blockquote 23,0,0,0,0 —> 
К слову, золотое сечение угадывается даже в форме галактики.
p, blockquote 24,0,0,0,0 —>
Спираль заслуженно носит звание «Кривой жизни», ведь её причудливая форма имеет место и угадывается во многих областях. Это настоящий символ эволюции, ибо нет такого объекта, чьё развитие не двигалось бы по спирали.
p, blockquote 25,0,0,0,0 —> p, blockquote 26,0,0,0,1 —>
И лишнее тому подтверждение — существование Золотого прямоугольника, что при разбиении на более мелкие прямоугольники в соответствии с последовательностью Фибоначчи с последующим разделением их в идентичной пропорции и далее, будет получена система под говорящим названием спираль Фибоначчи.
Источник