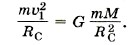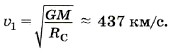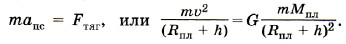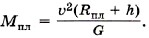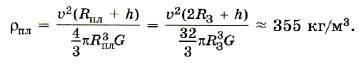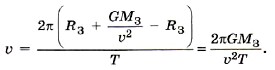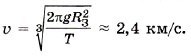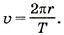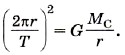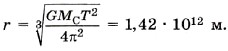§ 32. Примеры решения задач по теме «Первая космическая скорость
Для решения задач требуется знать закон всемирного тяготения, закон Ньютона, а также связь линейной скорости тел с периодом их обращения вокруг планет. Обратите внимание на то, что радиус траектории спутника всегда отсчитывается от центра планеты.
Задача 1. Вычислите первую космическую скорость для Солнца. Масса Солнца 2 • 10 30 кг, диаметр Солнца 1,4 • 10 9 м.
Р е ш е н и е. Спутник движется вокруг Солнца под действием единственной силы — силы тяготения. Согласно второму закону Ньютона запишем:
Из этого уравнения определим первую космическую скорость, т. е. минимальную скорость, с которой надо запустить тело с поверхности Солнца, чтобы оно стало его спутником:
Задача 2. Вокруг планеты на расстоянии 200 км от её поверхности со скоростью 4 км/с движется спутник. Определите плотность планеты, если её радиус равен двум радиусам Земли (Rпл = 2R3).
Р е ш е н и е. Планеты имеют форму шара, объём которого можно вычислить по формуле 
где Мпл — масса планеты, Rпл — её радиус.
Спутник движется вокруг планеты по круговой орбите. На него действует сила тяготения Fтяг, которая определяет центростремительное ускорение.
Согласно второму закону Ньютона
Из последнего уравнения находим массу планеты:
Подставив это выражение в формулу (1), имеем
Задача 3. При какой скорости спутника период его обращения вокруг Земли равен двум суткам?
Р е ш е н и е. Скорость спутника
где h — высота спутника над поверхностью Земли.
Для определения скорости необходимо знать высоту h.
Спутник движется по круговой орбите, при этом сила тяготения является центростремительной силой. Согласно второму закону Ньютона для спутника запишем:
где m — масса спутника.
Из уравнения (2) находим высоту 
Для упрощения расчётов поместим спутник на полюс, где сила тяжести равна силе тяготения. Тогда 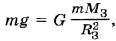
Подставив найденное выражение в формулу (3), определим скорость:
Задача 4. Определите среднее расстояние от Сатурна до Солнца, если период обращения Сатурна вокруг Солнца равен 29,5 лет. Масса Солнца равна 2 • 10 30 кг.
Р е ш е н и е. Считаем, что Сатурн движется вокруг Солнца по круговой орбите. Тогда согласно второму закону Ньютона запишем:
где m — масса Сатурна, r — расстояние от Сатурна до Солнца, Мс — масса Солнца.
Период обращения Сатурна 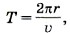
Подставив выражение для скорости υ в уравнение (4), получим
Из последнего уравнения определим искомое расстояние от Сатурна до Солнца:
Сравнив с табличными данными, убедимся в правильности найденного значения.
Задачи для самостоятельного решения
1. Определите длительность года на Венере. Среднее расстояние от Венеры до Солнца 1,08 • 10 8 км, а от Земли до Солнца 1,49 • 10 8 км.
2. Какой импульс силы подействовал на спутник массой 1 т, если спутник перешёл с орбиты радиусом R3 + h на орбиту радиусом R3 + 2h, где высота h равна 200 км?
3. Астероид вращается вокруг Солнца с периодом, равным 410 сут. Определите расстояние от астероида до Солнца.
Образцы заданий ЕГЭ
С1. Чему равен радиус кольца Сатурна, в котором частицы движутся со скоростью 10 км/с? Масса Сатурна 5,7 • 10 26 кг.
С2. Среднее расстояние от планеты Земля до Солнца составляет 149,6 млн км, а от планеты Юпитер до Солнца — 778,3 млн км. Чему равно отношение υЗ/υЮ линейных скоростей этих двух планет при их движении вокруг Солнца, если считать их орбиты окружностями?
С3. Среднее расстояние от Солнца до планеты Уран составляет 2875,03 млн км, а до планеты Земля — 149,6 млн км. Чему приблизительно равна средняя линейная скорость планеты Уран при её движении вокруг Солнца, если известно, что средняя скорость движения Земли по орбите вокруг Солнца составляет 30 км/с?
С4. Средняя плотность некоторой планеты равна средней плотности планеты Земля, а радиус этой планеты в 2 раза больше радиуса Земли. Определите отношение первой космической скорости на этой планете к первой космической скорости на Земле υп/υ3.
Источник
Среднее расстояние от планеты Земля до Солнца составляет 149,6 млн км ,а от планеты Юпитер до Солнца-778,3 млн км . Чему равно отношение Vз/Vю линейных скоростей этих двух планет при их движении вокруг Солнца если считать их орбиты Окружностью ?
Период обращения Земли вокруг Солнца
T₁ = 1 год
Период обращения Юпитера вокруг Солнца
T₂ = 11,86 лет
R₁ = 149,6 млн. км.
R₂ = 778,3 млн. км.
____________
V₁/V₂ — ?
Используем формулу:
V = 2π*R/T
V₁/V₂ = R₁*T₂ / (R₂*T₁) = 149,6*11,86 / (778,3*1) ≈ 2,28
Нет, это же против определения адиабатического процесса
Этот процесс как раз и определяется, как процесс, в котором газ не обменивается энергией с окружающей средой
m=1,8т v=10+0,5t т/кF?
Рассмотрим движение вдоль оси ОУ.
υy = υ*sin α = υ*sin 30° = 0,5*υ
начальная скорость 0,5*υ
конечная скорость υ = корень(2*2h*g), свободное падение с высоты 2h
используем формулу υ² — υ₀² = 2*g*Δr, где Δr — перемещение равное h
получаем 2*2h*g — 0,25*υ² = 2*g*h
4*g*h — υ²/4 = 2*g*h => h = υ²/(8*g)
теперь запишем кинематическое уравнение движения вдоль оси ОУ, с учетом, что начальная координата у₀ = h, а конечная у = 0
y₀ + υy*t — g*t²/2 = 0
h + υ*sin α*t — g*t²/2 = 0
υ²/(8*g) + 1/2*υ*t — g*t²/2 = 0, считаем g = 10 м/с², t = 4 с
υ²/80 + 2*υ — 80 = 0, решаем квадратное уравнение и получаем
υ² + 160*υ — 6400 = 0, откуда υ ≈ 33,1 м/с
Если не так, то жду комментарии!
Источник