Глава 1. Расширяющаяся Вселенная
§ 1. Крупномасштабная однородность и изотропия Вселенной
Любые попытки построения модели окружающего нас мира начинаются, конечно, с осмысливания наблюдений.
Что представляет собой наблюдаемая нами Вселенная?
В этом вводном параграфе мы ограничимся только самыми общими выводами из наблюдений, необходимыми для понимания дальнейшего. Более подробно с данными наблюдений мы познакомимся далее в § 8, 9 гл. 1.
До последнего времени астрономы могли наблюдать непосредственно лишь светящиеся тела, т. е. звезды, светящийся газ, звездные системы.
В сравнительно небольших масштабах звезды распределены в пространстве совершенно неравномерно. Это стало ясно с того времени, когда поняли, что Млечный Путь является гигантским скоплением звезд — Галактикой. По мере того, как сила телескопов возрастала и совершенствовались методы астрофизических исследований, выяснилось, что галактик много, что они распределены неравномерно, и что общая картина Вселенной представляется совокупностью отдельных скоплений галактик. Размеры скоплений и количество галактик в них бывают весьма различны. Большие скопления содержат тысячи галактик и имеют размеры в несколько мегапарсек (Мnс) * .
* ( В астрономии используется единица длины парсек (nс): 1 парсек = 3,1*10 18 см. В космологии употребляется единица длины Мегапарсек, равная 10 6 nс.)
Среднее расстояние между большими скоплениями около 30 Мnс, т. е. примерно в 10 раз больше, чем размеры скоплений. Это означает, что средняя плотность каждой структурной единицы в 100-1000 раз больше, чем та плотность, которая бы получилась, если бы все вещество равномерно «размазать» по всему пространству. Имеются и более крупные сгущения — сверхскопления. Таким образом, в масштабе 30 Мnс имеются отдельные структурные единицы, и, следовательно, Вселенная неоднородна. Если взять в 10 раз больший масштаб, то в таком кубе, где бы его ни помещать во Вселенной, будет примерно одно и то же количество скоплений галактик (примерно около 1000), т. е. в большом масштабе Вселенная приблизительно однородна. Пока исследовались скопления галактик с помощью оптических телескопов, мы не достаточно глубоко проникали в пространство, так как телескопы позволяют исследовать даже наиболее яркие объекты на расстояниях не более нескольких миллиардов парсек. Такой объем содержит порядка миллиона скоплений галактик. Точность оптических методов определений распределения галактик в пространстве не слишком велика и утверждение о том, что мир в среднем однороден, имело точность около 10-20%. За последнее десятилетие появились новые методы исследования крупномасштабной однородности и изотропии (так называют независимость свойств от направления в пространстве) Вселенной. Они связаны в первую очередь с измерением так называемого реликтового радиоизлучения, приходящего к нам с огромных расстояний. Мы подробно будем говорить дальше об этом излучении. Сейчас же отметим, что самые точные сегодняшние измерения не обнаружили отклонений в интенсивности этого излучения в разных направлениях на небе с относительной точностью в 10 -3 ÷10 -4 * .
* ( Мы не касаемся здесь небольшой неодинаковости интенсивности реликтового излучения в двух противоположных направлениях на небе, вызванных движением Солнца со скоростью около 360 км /сек относительно совокупности всех других галактик.)
Это свидетельствует о том, что свойства Вселенной одинаковы по всем направлениям, т. е., что Вселенная изотропна с высокой точностью. Но эти наблюдения, как мы увидим далее, свидетельствуют также и о том, что Вселенная с высокой точностью однородна. Отклонения в плотности распределения вещества от среднего значения в масштабах 1000 Мnс не превышают трех процентов, а в больших масштабах эти отклонения еще существенно меньше.
Таким образом, важнейшей наблюдаемой особенностью Вселенной является неоднородность, структурность в малом масштабе и однородность в большом масштабе.
В масштабах сотни мегапарсек вещество Вселенной можно рассматривать как однородную непрерывную среду, «атомами» которой являются галактики или скопления галактик.
В прошлом веке делались попытки построения так называемых иерархических моделей Вселенной. Согласно таким моделям во Вселенной имеется бесконечная последовательность систем все более высокого порядка: звезды объединены в галактики, галактики в скопления галактик, скопления образуют сверхскопления и т. д. до бесконечности. Наблюдения опровергают такое предположение.
При рассмотрении крупномасштабной структуры Вселенной надо исходить из свойств ее однородности и изотропии.
Наши работы с mitsubishi lancer 9 тюнинг Стингер-шоп.
Источник
Изотропность пространства — это одно из фундаментальных свойств Вселенной
Наиболее фундаментальная форма существования материи во Вселенной – пространственно-временной континуум – обладает набором свойств, определяющих облик нашего мира и общий характер протекающих в нем процессов. К числу таких основополагающих категорий относятся однородность и изотропность пространства. Это свойства, из которых, как мы увидим ниже, вытекают важнейшие для познания Вселенной следствия.
Понятие об однородности и изотропности
Однородность означает отсутствие в пространстве выделенных точек. Все местоположения одинаковы и равноправны по отношению к действию законов природы, и последние не изменяются при переходе (трансляции) из одной точки в другую. То есть, в пространстве Вселенной на всем его протяжении действуют одни и те же законы, и параллельный перенос любой замкнутой физической системы никак не отразится на ее функционировании.
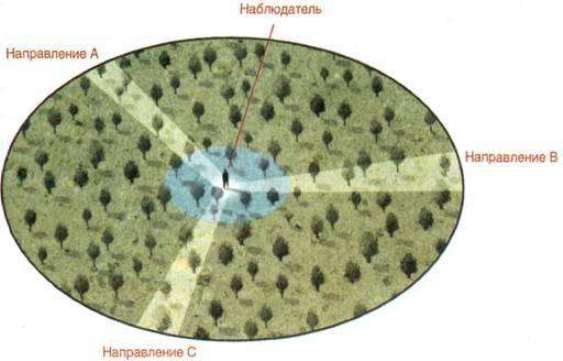
Изотропностью пространства называют отсутствие в нем выделенных, особых направлений. Какую бы ориентацию в пространстве мы ни избрали, на какой бы угол ни поворачивали систему отсчета, законы природы не изменят своего действия – все направления равноправны. Никакое изменение ориентации замкнутой системы не может повлиять на ее свойства.
Пространство и время в ньютоновской физике
Однородность и изотропность пространства – это ключевые понятия классической механики Галилея и Ньютона. Пространство в рамках этого учения мыслилось бесконечным, плоским, однородным, изотропным и абсолютным, то есть совершенно безразличным к распределению материи в нем. Пространство полагалось существующим только в качестве некоего места, где расположены физические тела, взаимодействующие между собой – но не со своим «вместилищем». Такое пространство могло служить идеальной, независимой ни от чего инерциальной системой отсчета.
Что касается времени, то его ньютоновская концепция определяет время также как некую самостоятельную, абсолютную категорию, относящуюся исключительно к длительности различных процессов. Время в ньютоновском понимании равномерно и синхронно для всей Вселенной, оно отделено от материи, от движущихся тел.
О свойствах времени
Необходимо сказать еще несколько слов о времени. Поскольку время одномерно, оно может иметь два равноправных направления – это означало бы его полную обратимость, а значит, абсолютную изотропность и пространства, и времени. Однако за некоторыми особыми исключениями, относящимися к явлениям в мире элементарных частиц, мы не наблюдаем в природе обратимых процессов. Вселенная эволюционирует в одном направлении, заданном так называемой «стрелой времени». Это понятие связано с термодинамикой Вселенной как замкнутой системы, имевшей определенные начальные условия развития.
Время, таким образом, будучи однородным, поскольку в нем не имеется выделенных моментов (все точки на оси времени равноправны), не является изотропным.
Однородность и изотропность пространства-времени
Специальная теория относительности показала, что пространство и время не абсолютны и не отделены друг от друга, а представляют собой тесно взаимосвязанные категории, участвующие в движении материи. Пространство-время представляет собой четырехмерный континуум – топологическое многообразие, точками которого являются не местоположения и моменты отдельно и независимо друг от друга, а события, определяемые четырьмя координатами в конкретной системе отсчета.
Общая теория относительности дополнила представления о пространстве-времени, рассматривая его как объект, тесно связанный с распределением и поведением движущихся масс материи – вещества и полей. Может показаться, что такое понимание противоречит тезису об изотропности пространства. Это, однако, не так. В четырехмерном континууме нет выделенных событий, все они равноправны по отношению к законам природы, поэтому пространство-время однородно. В некотором смысле можно говорить и о своеобразной изотропии континуума, так как время в нем тесно увязано с пространством. Но термодинамическая «стрела времени» накладывает весьма жесткое (хотя и вероятностное по характеру) ограничение на изотропность времени.
Изотропия как проявление симметрии
Так же, как и однородность, изотропность пространства – это отражение симметрии, фундаментального свойства, присущего основным законам Вселенной. Симметрия, или инвариантность в широком, физическом смысле означает, что характеризующие систему параметры не меняются после того, как данная система претерпела определенные преобразования. Так, однородность есть проявление трансляционной симметрии.
Существует также вращательная инвариантность, или симметрия поворота, которой подчиняется пространство. Именно она проявляется в форме изотропности.
Симметрия и законы сохранения
Все симметрии связаны с законами (иногда даже говорят о принципах – всеобщих закономерностях) сохранения. Например, однородность времени, то есть независимость от момента, в который существует физическая система, влечет за собой принцип сохранения энергии, однородность пространства – закон сохранения импульса (количества движения).
Следствием изотропности пространства является закон сохранения момента количества движения (углового, или кинетического момента). Это значит, что количество вращательного движения замкнутой системы безразлично к углу ее поворота относительно любой выбранной оси. Можно говорить также о прямолинейном движении системы мимо произвольной точки. Относительно нее наша система тоже обладает угловым моментом.
Часто возникающее недоумение по поводу изотропности (и однородности) вызвано обычно тем, что, наблюдая Вселенную на любом масштабе, мы видим, что вещество распределено и движется в ней крайне неоднородно и в различных точках, и в различных направлениях. Чтобы рассеять недоумение, достаточно представить себе, что далекая галактика переместилась или что мы убрали вазу со стола – ведь после этого в том направлении законы физики не перестали выполняться. Точно так же они будут работать независимо от того, проедет ли автомобиль мимо дома или на какой высоте и в какой плоскости расположена орбита спутника.
Источник
Свойства вселенной однородность изотропность
Наш беглый обзор мы начнем с краткого обсуждения современного состояния Вселенной (точнее, наблюдаемой ее части).
1.2.1. Однородность и изотропия
На больших масштабах видимая часть современной Вселенной однородна и изотропна. Размеры самых больших структур во Вселенной — сверхскоплений галактик и гигантских «пустот» (voids) — достигают десятков мегапарсеков). Области Вселенной размером 100 Мпк и более выглядят все одинаково (однородность), при этом выделенных направлений во Вселенной нет (изотропия). Эти факты сегодня надёжно установлены в результате глубоких обзоров, в которых наблюдались сотни тысяч галактик.
Сверхскоплений известно более 20. Местная группа входит в состав сверхскопления с центром в скоплении Девы. Размер сверхскопления около 40 Мпк, и помимо скопления Девы в него входят скопления из созвездий Гидра и Центавр. Эти наиболее крупные структуры уже очень «рыхлые»: плотность галактик в них всего в 2 раза превышает среднюю. До центра следующего сверхскопления, расположенного в созвездии Волосы Вероники, около сотни мегапарсеков.
В настоящее время ведётся работа по составлению наиболее крупного каталога галактик и квазаров — каталога SDSS (Sloan Digital Sky Survey). В его основе лежат данные, полученные с помощью 2,5-метрового телескопа, способного одновременно в 5 частотных диапазонах (длины волн света $\lambda = 3800-9200 A$, область видимого диапазона) измерять спектры 640 объектов. На этом телескопе предполагалось измерить положение и светимость более двухсот миллионов астрономических объектов и определить расстояния до более $10^6$ галактик и более $10^5$ квазаров. Полная зона наблюдения составила почти четверть небесной сферы. На сегодняшний день обработана большая часть экспериментальных данных, что позволило определить спектры около 675 тыс. галактик и более 90 тыс. квазаров. Результаты проиллюстрированы на рис. 1.1, где приведены ранние данные SDSS: положения 40 тыс. галактик и 4 тыс. квазаров, обнаруженных на участке небесной сферы площадью 500 квадратных градусов. Хорошо различимы скопления галактик и пустоты, изотропия и однородность Вселенной начинают проявляться на масштабах порядка 100 Мпк и больше. Цвет точки определяет тип объекта. Доминирование того или иного типа обусловлено, вообще говоря, процессами образования и эволюции структур — это асимметрия временная, а не пространственная.
Действительно, с расстояния 1,5 Гпк, на которое приходится максимум в распределении ярких красных эллиптических галактик (красные точки на рис. 1.1), свет летел до Земли около 5 миллиардов лет. Тогда Вселенная была другой (например, Солнечной системы еше не было).
Эта временная эволюция становится заметной на больших пространственных масштабах. Еще одной причиной выбора объектов наблюдения является наличие у регистрирующих приборов порога чувствительности: на больших расстояниях регистрируются только яркие объекты, а самыми яркими постоянно излучающими свет объектами во Вселенной являются квазары.
Рис. 1.1. Пространственное распределение галактик и квазаров по данным SDSS [1]. Зелеными точками отмечены все галактики (в данном телесном угле) с яркостью, превышающей некоторую. Красные точки указывают галактики наибольшей светимости из удалённых скоплений, образующие довольно однородную популяцию; в сопутствующей системе отсчёта их спектр смещён в красную область по сравнению с обычными галактиками. Голубые и синие точки показывают расположение обычных квазаров. Параметр h примерно равен 0,7
1.2.1. Расширение
Вселенная расширяется: галактики удаляются друг от друга (Разумеется, это не относится к галактикам, находящимся в одном скоплении и гравитационно связанным друг с другом; речь идет о галактиках, достаточно удаленных друг от друга). Образно говоря, пространство, оставаясь однородным и изотропным, растягивается, в результате чего все расстояния увеличиваются.
Для описания этого расширения вводят понятие масштабного фактора $a(t)$, который увеличивается с течением времени. Расстояние между двумя удаленными объектами во Вселенной пропорционально $a(t)$, а плотность частиц убывает как $[a(t)]^<-3>$. Темп расширения Вселенной, т.е. относительное увеличение расстояний в единицу времени, характеризуется параметром Хаббла $$ H(t)=\frac<\dot(t)>
Параметр Хаббла зависит от времени; для его современного значения применяем, как обычно, обозначение $H_0$.
Из-за расширения Вселенной увеличивается и длина волны фотона, испущенного в далёком прошлом. Как и все расстояния, длина волны растёт пропорционально $a(t).$ В результате фотон испытывает красное смещение. Количественно красное смещение z связано с отношением длин волн фотона в момент испускания и в момент поглощения $$ \frac<\lambda_
Разумеется, это отношение зависит от того, когда фотон был испущен (считая, что поглощается он на Земле сегодня), т.е. от расстояния между источником и Землей. Красное смещение — непосредственно измеряемая величина: длина волны в момент излучения определяется физикой процесса (например, это длина волны фотона, испускаемого при переходе атома водорода из первого возбуждённого состояния в основное), а $\lambda_
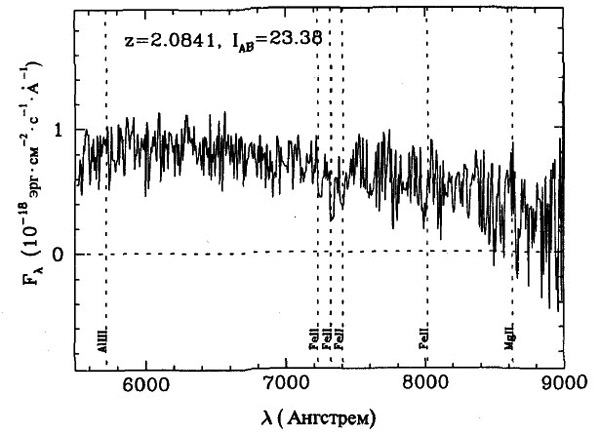
Реально идентификация осуществляется сразу по нескольким линиям, наиболее характерным для объектов того или иного типа (см. рис. 1.2). Если в спектре найдены линии поглощения (провалы, как в спектрах на рис. 1.2), это означает, что объект, у которого определяется красное смещение, расположен между источником излучения (например, квазаром) и наблюдателем (Фотоны вполне определённых частот испытывают резонансное поглощение на атомах и ионах (с последующим изотропным переизлучением), что и приводит к провалам в спектре интенсивности излучения в направлении на наблюдателя). Если же в спектре обнаружены линии излучения (пики в спектре), то объект сам является излучателем.
Рис. 1.2. Линии поглощения в спектрах далеких галактик [2]. На верхней диаграмме приведены результаты измерений дифференциального потока энергии от далекой (z = 2,0841) галактики. Вертикальные линии указывают расположение атомных линий поглощения, идентификация которых позволила определить красное смещение галактики. В спектрах более близких галактик эти линий лучше различимы. Диаграмма со спектрами таких галактик, уже приведёнными в сопутствующую систему отсчёта с учётом красного смещения, представлена на нижнем рисунке
Для $z\ll 1$ справедлив закон Хаббла $$ z=H_0 r,\,\,\, z\ll 1, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, (1.4) $$ где $r$ — расстояние до источника, a $H_0$ — современное значение параметра Хаббла. При больших z зависимость расстояния от красного смещения усложняется, что будет подробно обсуждаться.
Определение абсолютных расстояний до удалённых источников — весьма непростое дело. Один из методов состоит в измерении потока фотонов от удалённого объекта, чья светимость заранее известна. Такие объекты в астрономии иногда называют стандартными свечами.
Систематические ошибки в определении $H_0$ не очень хорошо известны и, по-видимому, довольно велики. Достаточно отметить, что величина этой постоянной, определённая самим Хабблом в 1929 году, составляла 550 км/(с · Мпк). Современные методы измерения параметра Хаббла дают 5 $$ H_0=73_<-3>^<+4>\frac
Проясним смысл традиционной единицы измерения параметра Хаббла, фигурирующей в (1.5). Наивная интерпретация закона Хаббла (1.4) состоит в том, что красное смещение обусловлено радиальным движением галактик от Земли со скоростями, пропорциональными расстояниям до галактик, $$ v=H_0r,\,\,\, v\ll 1, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, (1.6) $$
Тогда красное смещение (1.4) интерпретируется как продольный эффект Допплера (при $v\ll c$, т. е. $v\ll 1$ в естественных единицах, допплеровское смещение $z=v$). В связи с этим параметру Хаббла $H_0$ приписывают размерность [скорость/расстояние]. Подчеркнём, что интерпретация космологического красного смещения в терминах эффекта Допплера необязательна, а в ряде случаев неадекватна. Наиболее правильно использовать соотношение (1.4) в том виде, в каком оно написано. Величину $H_0$ традиционно параметризуют следующим образом: $$ H_0=h\cdot 100\frac
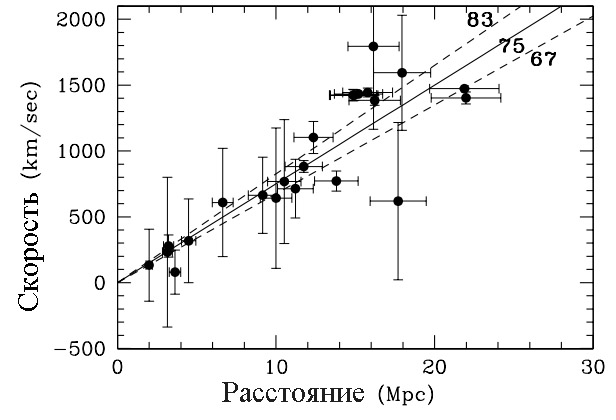
Рис. 1.3. Диаграмма Хаббла, построенная по наблюдению удаленных цефеид [6]. Сплошной линией показан закон Хаббла с параметром $H_0$ = 75 км/(с · Мпк), определенным в результате этих наблюдений. Пунктирные линии отвечают экспериментальным погрешностям в величине постоянной Хаббла
Для измерения параметра Хаббла в качестве стандартных свеч традиционно используют цефеиды — переменные звезды, чья переменность связана известным образом со светимостью. Связь эту можно выявить, изучая цефеиды в каких-нибудь компактных звездных образованиях, например, в Магеллановых Облаках. Поскольку расстояния до всех цефеид внутри одного компактного образования с хорошей степенью точности можно считать одинаковыми, отношение наблюдаемых яркостей таких объектов в точности равно отношению их светимостей. Период пульсаций цефеид может составлять от суток до нескольких десятков суток, за это время светимость изменяется в несколько раз. В результате наблюдений была построена зависимость светимости от периода пульсаций: чем ярче звезда, тем больше период пульсаций.
Цефеиды — гиганты и сверхгиганты, поэтому их удается наблюдать далеко за пределами Галактики. Изучив спектр удаленных цефеид, находят красное смещение по формуле (1.3), а исследуя временную эволюцию, определяют период пульсаций светимости. Затем, используя известную зависимость переменности от светимости, определяют абсолютную светимость объекта и далее вычисляют расстояние до объекта, после чего по формуле (1.4) получают значение параметра Хаббла. На рис. 1.3 приведена полученная таким образом диафамма Хаббла — зависимость красного смещения от расстояния.
Помимо цефеид, имеются и другие яркие объекты, используемые в качестве стандартных свеч, например сверхновые типа 1а.
1.2.3. Время жизни Вселенной и размер ее наблюдаемой части
Параметр Хаббла в действительности имеет размерность $[t^<-1>]$, поэтому современная Вселенная характеризуется временным масштабом $$ H_0^<-1>=\frac 1h\cdot \frac<1><100>\frac
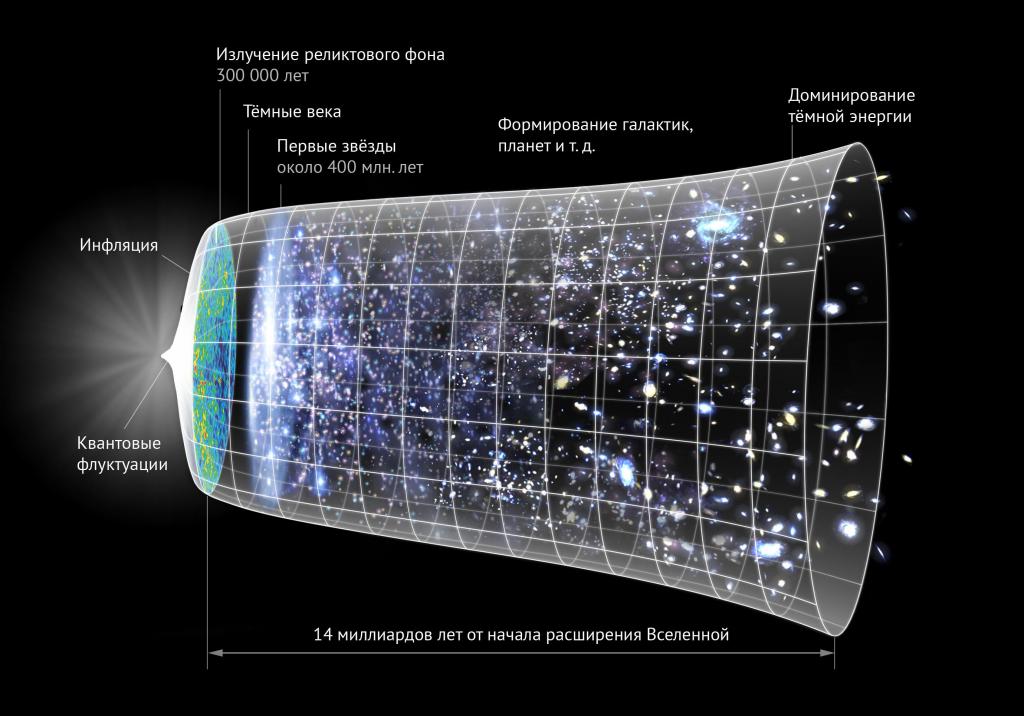
Грубо говоря, размер Вселенной увеличится вдвое за время порядка 10 млрд лет; галактики, находящиеся от нас на расстоянии порядка 3000 Мпк, удаляются от нас со скоростями, сравнимыми со скоростью света. Мы увидим, что время $H_0^<-1>$ по порядку величины совпадает с возрастом Вселенной, а расстояние $H_0^<-1>$ — с размером видимой части Вселенной. Мы будем уточнять представления о возрасте Вселенной и размере ее видимой части в дальнейшем. Здесь отметим, что прямолинейная экстраполяция эволюции Вселенной в прошлое (согласно уравнениям классической общей теории относительности) приводит к представлению о моменте Большого взрыва, с которого началась классическая космологическая эволюция; тогда время жизни Вселенной — это время, прошедшее с момента Большого взрыва, а размер видимой части (размер горизонта) — это расстояние, которое проходят с момента Большого взрыва сигналы, движущиеся со скоростью света. При этом размер всей Вселенной значительно превышает размер горизонта; в классической общей теории относительности пространственный размер Вселенной может быть и бесконечным.
Независимо от космологических данных, имеются наблюдательные ограничения снизу на возраст Вселенной $t_0$. Различные независимые методы приводят к близким ограничениям на уровне $t_0\gtrsim 14$ млрд лет $=1.4\cdot 10^<10>$.
Один из методов, с помощью которых получено последнее ограничение, состоит в измерении распределения белых карликов по светимости. Белые карлики — компактные звезды большой плотности с массами, примерно совпадающими с массой Солнца, — постепенно тускнеют в результате охлаждения посредством излучения. В Галактике встречаются белые карлики самых разных светимостей, однако начиная с некоторой низкой светимости число белых карликов резко падает, и это падение не связано с чувствительностью аппаратуры наблюдения. Объяснение состоит в том, что даже самые старые белые карлики еще не смогли настолько охладиться, чтобы стать такими тусклыми. Время охлаждения можно определить, изучая баланс энергии при охлаждении звезды. Это время охлаждения — возраст старейших белых карликов — является ограничением снизу на время жизни Галактики, а значит, и всей Вселенной.
Среди других методов отметим изучение распространённости радиоактивных элементов в земной коре и в составе метеоритов, сравнение эволюционной кривой звезд главной последовательности на диаграмме Герцшпрунга— Рассела («светимость — температура» или «яркость — цвет») с распространенностью старейших звезд в обедненных металлами шаровых скоплениях звезд (Шаровые скопления — внутригалактические структуры диаметром около 30 пк, включающие сотни тысяч и даже миллионы звезд. Термин «металлы» в астрофизике относится ко всем элементам тяжелее гелия.), изучение состояния релаксационных процессов в звездных скоплениях, измерение распространенности горячего газа в скоплениях галактик.
1.2.4. Пространственная плоскостность
Однородность и изотропия Вселенной не означают, вообще говоря, что в фиксированный момент времени трёхмерное пространство представляет из себя 3-плоскость (трёхмерное евклидово пространство), т. е. что Вселенная имеет нулевую пространственную кривизну. Наряду с 3-плоскостью, однородными и изотропными являются 3-сфера (положительная пространственная кривизна) и 3-гиперболоид (отрицательная кривизна). Фундаментальным результатом наблюдений последних лет стало установление того факта, что пространственная кривизна Вселенной если и отлична от нуля, то мала. Мы будем неоднократно возвращаться к этому утверждению, как для того, чтобы сформулировать его на количественном уровне, так и для того, чтобы изложить, какие именно данные свидетельствуют о пространственной плоскостности Вселенной. Здесь достаточно сказать, что этот результат получен из измерений анизотропии реликтового излучения и на качественном уровне сводится к тому, что радиус пространственной кривизны Вселенной заметно больше размера ее наблюдаемой части, т.е. заметно больше $H_0^<-1>$.
Отметим также, что данные по анизотропии реликтового излучения согласуются и с предположением о тривиальной пространственной топологии. Так, в случае компактного трёхмерного многообразия с характерным размером порядка хаббловского на небесной сфере наблюдались бы круги со схожей картиной анизотропии реликтового излучения — пересечения сферы последнего рассеяния фотонов, оставшихся после рекомбинации (образования атомов водорода), с образами этой сферы, получившимися в результате действия группы движения многообразия. Если бы пространство имело, например, топологию тора, то на небесной сфере наблюдалась бы пара таких кругов в диаметрально противоположных направлениях. Таких свойств реликтовое излучение не обнаруживает [7].
1.2.5. «Теплая» Вселенная
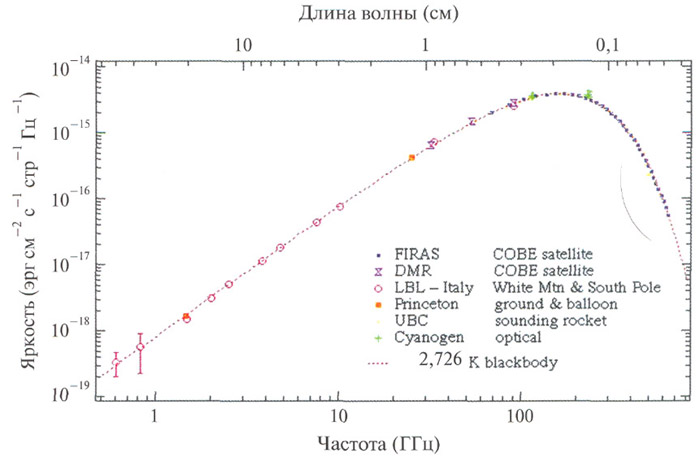
Современная Вселенная заполнена газом невзаимодействующих фотонов — реликтовым излучением, предсказанным теорией Большого взрыва и обнаруженным экспериментально в 1964 году. Плотность числа реликтовых фотонов составляет примерно 400 штук на кубический сантиметр. Распределение фотонов по энергиям имеет тепловой планковский спектр (рис. 1.4), характеризуемый температурой $$ T_0=2.725 \pm 0.001 K \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, (1.7) $$ (согласно анализу [9]). Температура фотонов, приходящих с разных направлений на небесной сфере, одинакова на уровне примерно $10^<-4>$; это — еще одно свидетельство однородности и изотропии Вселенной.
Рис. 1.4. Измерения спектра реликтового излучения. Компиляция данных выполнена в [8]. Пунктирной кривой показан планковский спектр (спектр «черного тела»). Недавний анализ [9] дает значение температуры (1.7), а не T = 2,726 К, как на рисунке
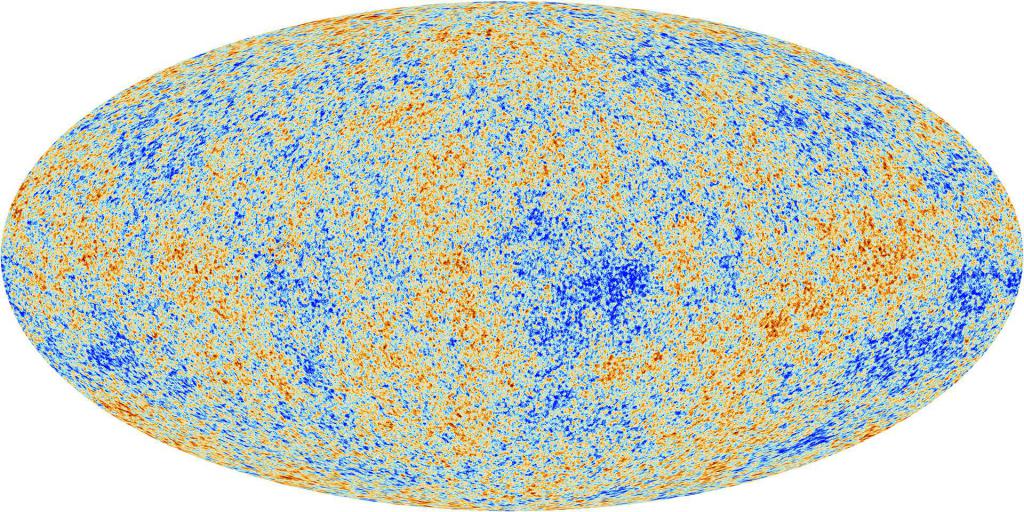
Рис. 1.5. Данные WMAP [5]: угловая анизотропия реликтового излучения, т. е. зависимость температуры фотонов от направления их прихода. Средняя температура фотонов и дипольная компонента (1.8) вычтены; изображенные вариации температуры находятся на уровне $\delta T \sim 100\mu K$ $\delta T/T_0\sim 10^<-4>-10^<-5>$
В то же время, экспериментально установлено, что эта температура все же зависит от направления на небесной сфере. Угловая анизотропия температуры реликтовых фотонов на данный момент хорошо измерена (см. рис. 1.5) и составляет, грубо говоря, величину порядка $\delta T/T_0\sim 10^<-4>-10^<-5>$. Тот факт, что спектр является планковским во всех направлениях, контролируется проведением измерений на разных частотах.
Мы будем неоднократно возвращаться к анизотропии (и поляризации) реликтового излучения, поскольку, с одной стороны, она несёт ценнейшую информацию о ранней и современной Вселенной, а с другой стороны, ее измерение возможно с высокой точностью.
Отметим, что наличие реликтового излучения позволяет ввести во Вселенной выделенную систему отсчёта: это та система отсчёта, в которой газ реликтовых фотонов покоится. Солнечная система движется относительно реликтового излучения в направлении созвездия Гидры. Скорость этого движения определяет величину дипольной компоненты анизотропии [10] $$ \delta T_
Современная Вселенная прозрачна для реликтовых фотонов (В действительности «прозрачности» разных частей Вселенной различаются. Например, горячий газ ($T\sim 10$ кэВ) в скоплениях галактик рассеивает реликтовые фотоны, которые приобретают при этом дополнительную энергию. Этот процесс приводит к «подогреву» реликтовых фотонов — эффекту Зельдовича—Сюняева. Величина этого эффекта невелика, но вполне заметна при современных методах наблюдений.): сегодня их длина свободного пробега велика по сравнению с размером горизонта $H_0^<-1>$. Это не всегда было так: в ранней Вселенной фотоны интенсивно взаимодействовали с веществом.
Поскольку температура реликтового излучения $T$ зависит от направления $\vec
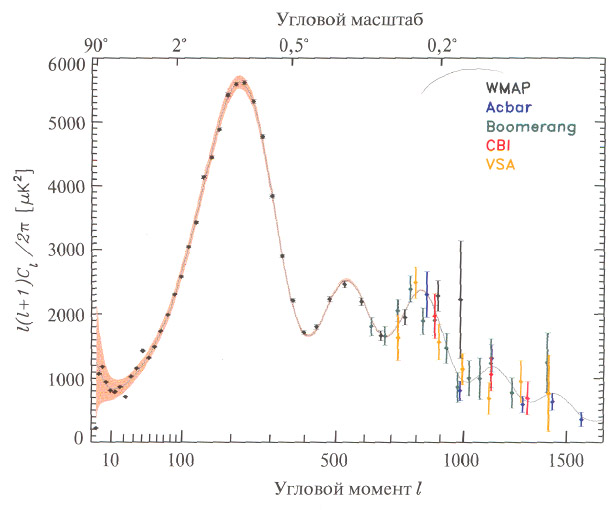
Рис. 1.6. Результаты измерений угловой анизотропии реликтового излучения различными экспериментами [5]. Теоретическая кривая получена в рамках модели $\Lambda$CDM.
Наблюдательные данные согласуются с тем, что флуктуации температуры $\delta T(\textbf
Таким образом, величина $\frac
Важно отметить, что измерение угловой анизотропии реликтового излучения даёт не одно экспериментально измеренное число, а целый набор данных, т. е. значения $C_l$ при различных $l$. Этот набор определяется целым рядом параметров ранней и современной Вселенной, поэтому его измерение даёт много космологической информации.
Источник