Вездесущая энтропия: от смерти Вселенной до груды грязной посуды
Михаил Петров
«Все процессы в мире происходят с увеличением энтропии» — эта расхожая формулировка превратила энтропию из научного термина в непреложное свидетельство обреченной борьбы человека с окружающим его беспорядком. Но что в оригинале скрывается за этой физической величиной? И как можно посчитать энтропию? «Теории и практики» попытались разобраться в этом вопросе и найти спасение от надвигающегося распада.
Термодинамика и «тепловая смерть»
Впервые термин «энтропия» в 1865 году ввел немецкий физик Рудольф Клаузиус. Тогда он имел узкое значение и использовался в качестве одной из величин для описания состояния термодинамических систем — то есть, физических систем, состоящих из большого количества частиц и способных обмениваться энергией и веществом с окружающей средой. Проблема заключалась в том, что до конца сформулировать, что именно характеризует энтропия, ученый не смог. К тому же, по предложенной им формуле можно было определить только изменение энтропии, а не ее абсолютное значение.
Упрощенно эту формулу можно записать как dS = dQ/T. Это означает, что разница в энтропии двух состояний термодинамической системы (dS) равна отношению количества тепла, затраченного на то, чтобы изменить первоначальное состояние (dQ), к температуре, при которой проходит изменение состояния (T). Например, чтобы растопить лед, нам требуется отдать ему некоторое количество тепла. Чтобы узнать, как изменилась энтропия в процессе таяния, нам нужно будет поделить это количество тепла (оно будет зависеть от массы льда) на температуру плавления (0 градусов по Цельсию = 273, 15 градусов по Кельвину. Отсчет идет от абсолютного нуля по Кельвину ( — 273° С ), поскольку при этой температуре энтропия любого вещества равна нулю). Так как обе величины положительны, при подсчете мы увидим, что энтропии стало больше. А если провести обратную операцию — заморозить воду (то есть, забрать у нее тепло), величина dQ будет отрицательной, а значит, и энтропии станет меньше.
Примерно в одно время с этой формулой появилась и формулировка второго закона термодинамики: «Энтропия изолированной системы не может уменьшаться». Выглядит похоже на популярную фразу, упомянутую в начале текста, но с двумя важными отличиями. Во-первых, вместо абстрактного «мира» используется понятие «изолированная система». Изолированной считается та система, которая не обменивается с окружающей средой ни веществом, ни энергией. Во-вторых, категорическое «увеличение» меняется на осторожное «не убывает» (для обратимых процессов в изолированной системе энтропия сохраняется неизменной, а для необратимых — возрастает).
За этими скучноватыми нюансами скрывается главное: второй закон термодинамики нельзя без оглядки применять ко всем явлениям и процессам нашего мира. Хороший тому пример привел сам Клаузиус: он считал, что энтропия Вселенной постоянно растет, а потому когда-нибудь неизбежно достигнет своего максимума — «тепловой смерти». Этакой физической нирваны, в которой не протекают уже никакие процессы. Клаузиус придерживался этой пессимистической гипотезы до самой смерти в 1888 году — на тот момент научные данные не позволяли ее опровергнуть. Но в 1920-х гг. американский астроном Эдвин Хаббл доказал, что Вселенная расширяется, а значит, ее
сложно назвать изолированной термодинамической системой. Поэтому современные физики к мрачным прогнозам Клаузиуса относятся вполне спокойно.
Энтропия как мера хаоса
Поскольку Клаузиус так и не смог сформулировать физический смысл энтропии, она оставалась абстрактным понятием до 1872 года — пока австрийский физик Людвиг Больцман не вывел новую формулу, позволяющий рассчитывать ее абсолютное значение. Она выглядит как S = k * ln W (где, S — энтропия, k — константа Больцмана, имеющая неизменное значение, W — статистический вес состояния). Благодаря этой формуле энтропия стала пониматься как мера упорядоченности системы.
Как это получилось? Статистический вес состояния — это число способов, которыми можно его реализовать. Представьте рабочий стол своего компьютера. Сколькими способами на нем можно навести относительный порядок? А полный беспорядок? Получается, что статистический вес «хаотичных» состояний гораздо больше, а, значит больше и их энтропия. Посмотреть подробный пример и рассчитать энтропию собственного рабочего стола можно здесь.
В этом контексте новый смысл приобретает второй закон термодинамики: теперь процессы не могут самопроизвольно протекать в сторону увеличения порядка. Но и тут не стоит забывать про ограничения закона.
Иначе человечество уже давно было бы в рабстве у одноразовой посуды. Ведь каждый раз, когда мы моем тарелку или кружку, нам на помощь приходит простейшая самоорганизация. В составе всех моющих средств есть поверхно-активные вещества (ПАВ). Их молекулы составлены из двух частей: первая по своей природе стремится к контакту с водой, а другая его избегает.
При попадании в воду молекулы «Фэйри» самопроизвольно собираются в «шарики», которые обволакивают частички жира или грязи (внешняя поверхность шарика это те самые склонные к контакту с водой части ПАВ, а внутренняя, наросшая вокруг ядра из частички грязи — это части, которые контакта с водой избегают). Казалось бы, этот простой пример противоречит второму закону термодинамики. Бульон из разнообразных молекул самопроизвольно перешел в некое более упорядоченное состояние с меньшей энтропией. Разгадка снова проста: систему «Вода-грязная посуда после вечеринки», в которую посторонняя рука капнула моющего средства, сложно считать изолированной.
Черные дыры и живые существа
Со времен появления формулы Больцмана термин «энтропия» проник практически во
все области науки и оброс новыми парадоксами. Возьмем, к примеру астрофизику и пару «черная дыра — падающее в нее тело». Ее вполне можно считать изолированной системой, а значит, ее энтропия такой системы должна сохраняться. Но она бесследно исчезает в черной дыре — ведь оттуда не вырваться ни материи, ни излучению. Что же происходит с ней внутри черной дыры?
Некоторые специалисты теории струн утверждают, что эта энтропия превращается в энтропию черной дыры, которая представляет собой единую структуру, связанную из многих квантовых струн (это гипотетические физические объекты, крошечные многомерные структуры, колебания которых порождают все элементарные частицы, поля и прочую привычную физику). Впрочем, другие ученые предлагают менее экстравагантный ответ: пропавшая информация, все-таки возвращается в мир вместе с излучением, исходящим от черных дыр.
Еще один парадокс, идущий вразрез со вторым началом термодинамики — это существование и функционирование живых существ. Ведь даже живая клетка со всеми ее биослоями мембран, молекулами ДНК и уникальными белками — это высокоупорядоченная структура, не говоря уже о целом организме. За счет чего существует система с такой низкой энтропией?
Этим вопросом в своей книге «Что такое жизнь с точки зрения физики» задался знаменитый Эрвин Шредингер, создатель того самого мысленного эксперимента с котом: «Живой организм непрерывно увеличивает свою энтропию, или, иначе, производит положительную энтропию и, таким образом, приближается к опасному состоянию максимальной энтропии, представляющему собой смерть. Он может избежать этого состояния, то есть оставаться живым, только постоянно извлекая из окружающей его среды отрицательную энтропию. Отрицательная энтропия — это то, чем организм питается».
Точнее организм питается углеводами, белками и жирами. Высокоупорядоченными, часто длинными молекулами со сравнительно низкой энтропией. А взамен выделяет в окружающую среду уже гораздо более простые вещества с большей энтропией. Вот такое вечное противостояние с хаосом мира.
Источник
Энтропия Вселенной и парадокс черных дыр
Знаменитый ученый Стивен Хокинг много размышлял о природе черных дыр. И еще он очень хотел найти связь между квантовой механикой и гравитацией. Это привело его к размышлениям об энтропии. Эта концепция настолько фундаментальна, что важна не только для физики повседневной жизни. Но и для понимания природы самого времени.
Энтропия
Что же такое энтропия? Если говорить простыми словами — это уровень беспорядка в какой-нибудь изначально упорядоченной системе. В принципе, ничего сложного. Омлет, например, имеет более высокую степень энтропии, чем яйцо, из которого он был изготовлен. Куча кирпичей и деревянных досок обладает большей энтропией, чем дом. Ведь каждый кирпич или доска находятся в нем на своем месте.
Принцип, согласно которому общая энтропия в системе (или во Вселенной) должна увеличиваться со временем, известен как Второй закон термодинамики.
Этот закон не говорит о том, что Вы не можете превратить кучу кирпичей и досок в дом. Или что разбитое яйцо нельзя собрать обратно, склеить скорлупу и покрасить его известью, что бы стало все как было. Он просто говорит о том, что уменьшение энтропии в одном месте ведет к увеличению энтропии в другом. Что это значит?
Пример. Вы строите дом из кучи кирпичей и досок. Уменьшая тем самым степень энтропии в каком-то локальном месте. В данном случае пусть это будут тещины 6 соток где-то под Чебоксарами. Забивая гвозди и складывая в нужном порядке кирпичи, Вы тратите энергию. Часть этой энергии будет проявляться в виде тепла, которое будет излучаться в окружающую среду. Что делает воздух вокруг Вас, образно говоря, «грязным». Частицы воздуха нагреются от выделяемого Вами тепла. А более высокие температуры означают более высокую энтропию. Потому что частицы начинают более энергично и хаотично двигаться случайным образом после нагревании.
Ваша работа неизбежно создаст достаточно энтропии, которое компенсирует упорядоченное расположение кирпичей.
Итак, о чем это мы? Ах, да. Какое отношение имеет вся эта история к черным дырам?
Черные дыры: мы то тут при чем?
И кандидаты в доктора начали задавать друг другу странные вопросы. Например: что будет, если взять объект, который имеет высокую энтропию, и бросить со всего размаху в черную дыру? Куда денется вся его энтропия? Мы что, только что нарушили Второй закон термодинамики, уменьшив количество энтропии во Вселенной? Но это же противоречит всем нашим знаниям и теориям!
Мохнатые бороды и седые головы приуныли. Единственная гипотеза, которую выдвинули физики, чтобы объяснить очевидный парадокс, говорила о том, что вероятнее всего сами черные дыры должны иметь какую-то энтропию.
Правила термодинамики гласят, что для того, чтобы иметь определенную энтропию, черная дыра должна иметь определенную температуру. И она должна производить какое-то тепло, которое может быть воспринято кем-то за ее пределами. Это означает, что должен существовать способ покинуть черную дыру. Что опять же противоречило официальной науке.
Чтобы разобраться во всех этих чудных делах, Хокинг совершил глубокое погружение в постулаты общей теории относительности и квантовой механики.
Когда он вынырнул оттуда, вид у него был усталый, но довольный. Были сделаны необходимые расчеты. И оказалось, что черные дыры должны излучать тепло, которое получило название излучение Хокинга. Это предсказание создало совершенно новые парадоксы. Которые физики не могут разрешить и по сей день.
Время течет непрерывно, уверенно и всегда в одну сторону
Но энтропия оказалась проблемой еще более глубокой. Многие физики утверждают, что неуклонное увеличение энтропии ответственно за направление течения самого времени. Большая часть физики прекрасно работает в прямом или обратном направлении времени. Однако энтропия увеличивается только в одну сторону. Поэтому мы можем помнить прошлое, но не можем предвидеть будущее. Лишь стрела времени определяет то, в каком направлении развивается энтропия.
В великих традициях физики каждое новое открытие создает все новые и новые вопросы. Соединение стрелы времени с ростом энтропии поднимает острый вопрос о том, как вообще Вселенной удалось родиться в состоянии, в котором энтропия была настолько низкой, что она смогла продолжать расти все прошедшее время.
У нас пока нет ответа на этот вопрос. Но мы надеемся, что он может помочь нам лучше понять, как возникла Вселенная. И какова будет ее судьба, когда энтропия достигнет своего максимального состояния. Будет ли это означать конец всех времен?
Источник
Энтропия Вселенной
Термодинамическая стрела времени подразумевает, что энтропия всегда возрастает, поэтому сегодня она больше, чем в прошлом
Второй закон термодинамики – один из тех загадочных законов природы, который возникает из ее фундаментальных правил. Он говорит о том, что энтропия, мера беспорядка во Вселенной, всегда должна увеличиваться в любой замкнутой системе.
Но как возможно, что наша Вселенная сегодня, которая выглядит организованной и упорядоченной с помощью планетных систем, галактик и сложной космической структуры, каким-то образом находится в состоянии с более высокой энтропией, чем сразу после Большого взрыва, ведь кажется, что все должно быть наоборот.
Термодинамическая стрела времени подразумевает, что энтропия всегда возрастает, поэтому сегодня она больше, чем в прошлом.
И все же, если мы думаем об очень ранней Вселенной, она, безусловно, выглядит как состояние с высокой энтропией! Вообразите это: море частиц, включая вещество, антивещество, глюоны, нейтрино и фотоны, все вокруг несутся с энергиями в миллиарды раз выше, чем даже БАК может получить сегодня. Их было так много – всего около 10 99 и все они находились в области размером с футбольный мяч. Прямо в момент Большого взрыва этот крошечный регион с этими чрезвычайно энергичными частицами вырастет во всю нашу наблюдаемую Вселенную в течение следующих 13,8 миллиардов лет.
Совершенно очевидно, что сегодня Вселенная намного холоднее, больше, более структурирована и однородна. Но мы можем фактически количественно оценить энтропию Вселенной в оба момента, в момент Большого взрыва и сегодня, с точки зрения постоянной Больцмана, kb. (kb = 1,380 649 * 10 -23 Дж/К)
В момент Большого взрыва почти вся энтропия была обусловлена излучением, а общая энтропия Вселенной составляла S = 10 88 kb. С другой стороны, если сегодня мы вычислим энтропию Вселенной, она будет примерно в четыре миллиарда раз больше: S = 10 103 kb. В то время как оба эти числа кажутся большими, первое число определенно имеет низкую энтропию по сравнению с последним: это всего лишь 0,0000000000001% от него!
Однако что важно иметь в виду, когда мы говорим об этих цифрах. Когда вы слышите такие термины, как «мера беспорядка», это на самом деле очень плохое описание того, что такое энтропия. Вместо этого представьте, что у вас есть любая система, которая вам нравится: материя, излучение, что угодно. Предположительно, там будет закодирована некоторая энергия, будь то кинетическая, потенциальная, энергия поля или любой другой тип энергии. Что на самом деле измеряет энтропия, так это количество возможных вариантов состояния вашей системы.
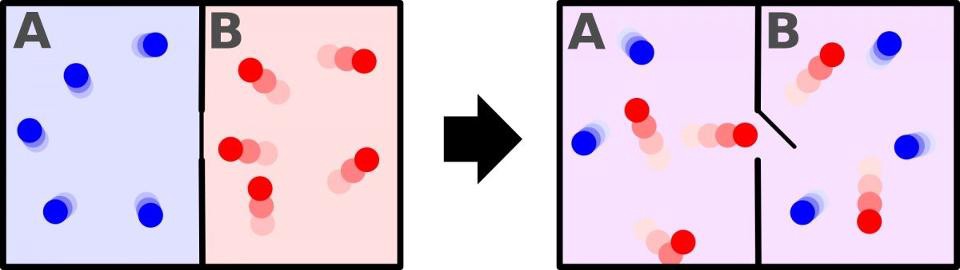
Если ваша система имеет, скажем, холодную часть и горячую часть, вы можете организовать ее меньшим количеством способов, чем если бы она была с одинаковой температурой. Система, слева вверху, является системой с более низкой энтропией, чем система справа.
Фотоны на космическом микроволновом фоне сегодня имеют практически ту же энтропию, что и при рождении Вселенной. Вот почему говорят, что Вселенная расширяется адиабатически, что означает постоянную энтропию. Хотя мы можем смотреть на галактики, звезды, планеты и т. д. и удивляться тому, насколько упорядоченными или беспорядочными они кажутся, их энтропия незначительна. Так что же вызвало это огромное увеличение энтропии?
Ответ – черные дыры. Если вы подумаете обо всех частицах, которые образуют черную дыру, то получите огромное их количество. Попадая в черную дыру, вы неизбежно получаете сингулярность. И число состояний прямо пропорционально массам частиц в черной дыре, поэтому, чем больше черных дыр вы сформируете (или чем массивнее будут черные дыры), тем больше энтропии вы получаете во Вселенной.
Одна только сверхмассивная черная дыра в центре Млечного Пути имеет энтропию S = 10 91 kb, что примерно в 1000 раз больше, чем у всей Вселенной при Большом Взрыве. Учитывая количество галактик и массу черных дыр в целом, общая энтропия сегодня достигла значения S = 10 103 kb.
И все это будет только ухудшаться! В далеком будущем будет образовываться все больше и больше черных дыр, и большие черные дыры, которые существуют сегодня, будут продолжать расти в течение следующих 10 20 лет.
Если бы мы превратили всю вселенную в черную дыру, мы бы достигли максимальной энтропии примерно S = 10 123 kb, или в 100 квинтиллионов раз больше, чем энтропия сегодня. Когда черные дыры распадутся в еще больших временных масштабах – примерно до 10 100 лет – эта энтропия останется почти постоянной, поскольку излучение черного тела (излучение Хокинга), создаваемое распадающимися черными дырами, будет иметь такое же количество возможных состояний, что и ранее существовавшая черная дыра.
Так почему же в ранней Вселенной была настолько низкая энтропия? Потому что там не было черных дыр. Энтропия S = 10 88 kb по-прежнему чрезвычайно велика, но это энтропия всей Вселенной, которая почти исключительно закодирована в остатке излучения (и, в несколько меньшей степени, нейтрино) от Большого взрыва. Поскольку объекты, которые мы видим, когда смотрим на Вселенную, такие как звезды, галактики и т. д., имеют незначительную энтропию по сравнению с этим оставшимся фоном, легко обмануть себя, полагая, что энтропия существенно изменяется в виде структурных форм, но это всего лишь совпадение, а не причина.
Если бы не было таких объектов, как черные дыры, энтропия Вселенной была бы почти постоянной на протяжении последних 13,8 миллиардов лет! То первичное состояние действительно имело значительную энтропию; просто у черных дыр ее намного больше.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Источник

