ИЗУЧЕНИЕ покрытий звезд Луной
Е.М.Трунковский
Статья О. И. Митина, Н. В. Кулаковой и С. В. Коробкина*) дает любителям астрономии хорошее первоначальное представление о том, как и зачем можно и нужно наблюдать покрытия звезд Луной. Сами по себе такие наблюдения весьма интересны и содержат даже некоторые элементы, свойственные ситуациям в спорте: ведь наблюдаемые события — покрытия или УоткрытияФ звезд Луной — очень скоротечны, их длительность во времени — малые доли секунды, и требуются хорошие наблюдательные навыки, быстрота и оперативность, чтобы не пропустить нужный момент, успешно провести наблюдение и выполнить необходимые измерения. Отмечу еще одно важное обстоятельство: наблюдения покрытий звезд Луной в некоторых отношениях подобны наблюдению полного солнечного затмения, длительность которого во времени не превышает нескольких минут; и хотя для Солнца продолжительность этого явления на 3-4 порядка превышает подобную величину, характерную для покрытий звезд, все же с точки зрения наблюдателя ситуация тоже весьма напряженная. Эта аналогия в действительности имеет гораздо более глубокую природу: ведь и в том, и в другом случае речь идет о затмении звезды (одна из затмеваемых звезд — наше Солнце) гораздо более близкой к нам Луной.
Замечательно то, что «в лице» нашего вечного спутника природа подарила нам прекрасный «космический экран», с помощью которого, почти как в физической (оптической) лаборатории, можно изучать не только структуру внешних слоев атмосферы Солнца (хромосферы и короны), но и, как мы увидим ниже, структуру атмосфер и оболочек некоторых звезд. Такая возможность в случае Солнца возникает благодаря тому удивительному (даже, можно сказать, загадочному) факту, что отношение линейного диаметра Луны (в километрах) к ее расстоянию от Земли в среднем почти точно совпадает с аналогичным отношением для Солнца (Солнце больше Луны примерно в 400 раз, но и дальше от нас в такое же количество раз). Другими словами, средние угловые размеры дисков Луны и Солнца на небе равны между собой и составляют примерно полградуса дуги. Этого никак нельзя сказать о других звездах, находящихся на таких гигантских расстояниях от нас, что даже самые большие из них по линейным размерам и наиболее близкие к нам имеют угловые диаметры не больше нескольких сотых долей секунды дуги. Однако оказывается, что такое огромное различие угловых размеров Луны и звезд тоже можно с успехом использовать при решении научных задач, т.к. в этом случае край Луны по отношению к звездам можно рассматривать как прямолинейный, а это позволяет получать ценную информацию как о движении и фигуре Луны, так и о координатах звезд и, что особенно важно, о самих покрываемых звездах.
Известно, что Луна в своем орбитальном движении вокруг Земли (точнее, вокруг центра масс системы Земля-Луна) медленно перемещается среди звезд с запада на восток со средней угловой скоростью около 0.5 секунды дуги за секунду времени. Линейная скорость движения Луны по орбите — около 1 км/сек. Понятно, что при таком движении лунный диск время от времени закрывает от наблюдателя свет тех или иных звезд. В фазах между новолунием и полнолунием происходят покрытия звезд темным краем диска Луны, а в фазах между полнолунием и следующим новолунием — покрытия светлым краем и «открытия», т.е. появления звезд из-за лунного диска, на его темном крае.
Ценность и важность высокоточной регистрации моментов покрытий звезд Луной была осознана астрономами уже несколько столетий назад. Достаточно сказать, что одним из важных стимулов создания в 1670 г. всемирно известной Гринвичской обсерватории была заинтересованность в точных измерениях положений лунного лимба относительно звезд (лимбом называют спроектированный на небесную сферу край диска Луны), в том числе путем регистрации моментов покрытий звезд краем Луны из разных пунктов на Земле: это позволяло определять координаты на поверхности Земли и успешно решать задачи навигации. Главная же причина того, что в ряде стран еще в 18-м веке были начаты программы массовой регистрации моментов покрытий звезд Луной, заключалась в том, что данные таких наблюдений были необходимы для уточнения теории движения Луны. Эта проблема возникла вскоре после появления в 1687 г. «Начал» Ньютона, где был предложен первоначальный вариант такой теории. При повышении точности астрономических наблюдений обнаружились расхождения с предсказаниями теории, и в 18-м веке целый ряд крупнейших ученых, таких как Бернулли, Эйлер, Клеро, Д’Аламбер, Лагранж и Лаплас, занимались усовершенствованием теории движения Луны путем учета всех возможных факторов, возмущающих ее орбиту. В XIX-м веке большой вклад в уточнение этой теории внес американский астроном Симон Ньюкомб, использовавший в своей работе данные регистрации моментов покрытий звезд Луной. В 1919 г. появилась теория Е. Брауна, которая до сих пор принимается за основу при предвычислениях положений Луны в различные моменты времени. Дальнейшие уточнения модели движения Луны базировались в основном опять-таки на использовании постоянно накапливающихся данных наблюдений покрытий Луной.
При регистрации момента покрытия с точностью, лучшей, чем 1 сек, можно, с учетом величины угловой скорости Луны, определить положение точки лунного лимба, в которой произошел контакт со звездой, с точностью порядка 0.5 угловой секунды. Хотя, казалось бы, подобная точность не так уж высока, наблюдения такого качества, которые во всем мире обычно проводятся любителями астрономии, могут внести и уже внесли решающий вклад в изучение долгопериодических составляющих движения Луны. К настоящему времени любители провели регистрацию десятков тысяч моментов покрытий звезд Луной при наблюдениях из различных мест, разбросанных по всей Земле. Это позволило создать непрерывно пополняющийся банк данных, роль которого в изучении различных составляющих движения Луны очень велика. Поэтому каждый, кто желает внести посильный вклад в развитие астрономической науки, в состоянии это сделать довольно простым способом, вооружившись всего лишь биноклем или небольшой зрительной трубой и точными часами с секундомером и проводя время от времени визуальные наблюдения покрытий ярких звезд темным краем Луны. Для выполнения таких наблюдений вполне достаточно информации, публикуемой в ежегодно издаваемой переменной части Астрономического календаря.
Важнейшим фактором, который обеспечивает возможность уверенной визуальной регистрации момента покрытия звезды Луной с точностью в десятые и даже сотые доли секунды, является практически полное отсутствие у Луны атмосферы. Еще в XIX-м веке астрономы обратили внимание на удивительно резкое, мгновенное исчезновение светового потока от звезд при покрытии их Луной. Это явление они справедливо рассматривали как важнейшее свидетельство того, что Луна лишена сколько-нибудь заметной устойчивой атмосферы.
Появление в современную эпоху фотоэлектрических приемников излучения и компьютеров позволило достичь точности регистрации моментов покрытий звезд Луной порядка нескольких миллисекунд (см. ниже). Это дает возможность определять положение данного участка лунного лимба на небесной сфере в момент покрытия с очень высокой точностью: например, если момент покрытия зарегистрирован с точностью 0.002 с и координаты звезды хорошо известны (с точностью не хуже 0.001 секунды дуги), то при типичной величине угловой скорости движения Луны 0.5 угл.сек. за секунду времени можно определить положение точки контакта на лунном лимбе в этот момент с точностью около 0.001 сек. дуги (это соответствует погрешности определения линейного расстояния в плоскости лунного края около 2 м). С другой стороны, если имеется хорошая теория, позволяющая очень точно предсказывать движение Луны, и есть подробные данные о профиле лунного лимба (т.е. хорошо изучен рельеф лунного края), то можно с точностью указанного порядка определить координаты звезды.
Представим себе теперь, что для звезд с хорошо известными координатами моменты их покрытий Луной зарегистрированы с высокой точностью. Если у нас есть хорошая теория движения Луны и достаточно подробная модель профиля лунного лимба, позволяющие надежно предвычислить эти моменты с учетом положений точек контактов на лимбе, то при сопоставлении рассчитанных и зарегистрированных моментов мы можем получить более точную информацию о рельефе соответствующих участков лунного края, т.е. о поверхности Луны. Говоря упрощенно, это значит, что в случае, когда действительный момент покрытия на какое-то мгновение опережает предвычисленный, в точке контакта присутствует выступ лунной поверхности («горка»), не учтенный в модели профиля лимба, а если обнаружено «отставание» наблюдаемого момента, то в месте покрытия существует неучтенная «впадина». На самом деле ситуация сложнее, т.к. при выполнении предвычислений может быть несколько не полностью учтенных факторов, и достоверность обнаружения неровностей лунной поверхности зависит от того, какова реальная точность предвычислений. Сама по себе задача проведения максимально точных предвычислений очень сложна из-за необходимости учитывать множество различных факторов.
Поскольку видимые угловые размеры лунного диска зависят от расстояния между наблюдателем и центром Луны, ясно, что высокоточные определения моментов покрытий дают возможность уточнить данные о расстоянии до Луны в различных точках ее орбиты.
Как видим, наблюдения покрытий звезд Луной, несмотря на достаточную простоту этого метода, дают весьма разнообразную и ценную астрономическую информацию. Но, пожалуй, самым интересным применением этого метода для решения серьезных научных задач являются прямые измерения угловых размеров различных звезд путем анализа кривых блеска, зарегистрированных при наблюдениях их покрытий темным краем Луны.
Легко подсчитать, что если диск звезды в проекции на небесную сферу имеет угловой диаметр 0.005 угл.сек. (это типичная величина для сравнительно близких звезд-гигантов и сверхгигантов), то при названной выше величине угловой скорости край Луны «проскочит» звездный диск примерно за 0.01 сек. Это дает представление об интервале времени, в течение которого световой поток от звезды должен сильно уменьшиться. Отсюда следует, что для успешного измерения углового диаметра звезды необходимо иметь аппаратуру, которая бы очень быстро (как говорят, с высоким разрешением по времени) регистрировала изменения светового потока от звезды. И если бы все было так просто, как это выглядит в рамках законов геометрической оптики, то задача свелась бы к измерению короткого промежутка времени, за который световой поток от звезды падает от первоначального значения до нуля. Такую идею впервые высказал в 1908 г. британский офицер П. Мак-Магон. Однако природа, как правило, оказывается устроенной сложнее, чем нам бы того хотелось, и весьма неохотно позволяет человеку добывать новые знания о своих законах и объектах. Дело в том, что при рассмотрении процесса покрытия звезды Луной нельзя применять законы геометрической оптики, здесь работают другие принципы — принципы волновой оптики. А из них следует, что в данном случае возникают явления дифракции света звезды на крае лунного диска, и в результате кривая изменения светового потока приобретает гораздо более сложный характер. На это сразу же после публикации идеи Мак-Магона обратил внимание выдающийся английский астрофизик Артур Эддингтон. Из анализа, проведенного Эддингтоном, астрономы сделали вывод, что красивая идея Мак-Магона, увы, неосуществима на практике, т.к. дифракция мешает измерять угловые размеры звезд.
Однако, как это неоднократно случалось в истории науки, однажды высказанная идея не пропала бесследно и примерно через четверть века обрела новую жизнь. В 30-е годы несколько астрономов в разных странах, в том числе наш соотечественник С. Г. Натансон, пришли к выводу, что сама дифракционная картина покрытия должна содержать информацию об угловом размере звезды. Из теории дифракции следует, и это было подтверждено наблюдениями в конце тех же 30-х годов, что дифракционная кривая покрытия звезды, имеющей хоть и очень малый, но все же конечный угловой диаметр, несколько отличается от аналогичной кривой для точечного источника (т.е. воображаемого бесконечно удаленного источника, угловой размер которого можно считать строго равным нулю). И если у вас есть телескоп с зеркалом достаточного диаметра и чувствительная приемная аппаратура, позволяющая регистрировать изменения светового потока при покрытии с высоким временным разрешением (порядка 0.001 сек), т.е. проводить высокоскоростную фотометрию, вы имеете шанс получить достаточно хорошую дифракционную кривую, при анализе которой можно выявить ее отличия от кривой покрытия точечного источника.
О том, как проводятся подобные наблюдения и соответствующий, довольно сложный, анализ полученных данных, можно прочитать в статье М. Б. Богданова, Е. М. Трунковского и А. М. Черепащука в журнале «Земля и Вселенная», 1992, N6, с. 3-11. Важно, что при обработке кривых покрытий, полученных с помощью высокоскоростной фотоэлектрической фотометрии и «привязанных» к сигналам точного времени, можно с точностью до миллисекунды определить момент геометрического покрытия центра звездного диска краем Луны. В случае точечного источника этот момент соответствует той точке дифракционной кривой, в которой величина светового потока от него падает до 1/4 от первоначального значения. Для звезды с конечным угловым диаметром этот момент будет несколько смещен по сравнению с точечным источником и его можно найти после соответствующей обработки как «побочный продукт» решения задачи по определению углового диаметра звезды.
Фотоэлектрические наблюдения покрытий звезд Луной проводятся во многих обсерваториях мира, начиная с 50-х годов. К настоящему времени этим методом измерены угловые диаметры примерно полутора сотен звезд, а также обнаружено много тесных двойных звезд с угловыми расстояниями между компонентами, составляющими сотые и даже тысячные доли секунды дуги; другими существующими в настоящее время методами измерить столь малые величины угловых диаметров в подавляющем большинстве случаев невозможно, а обнаружить настолько тесные двойные звезды и определить их параметры во многих случаях тоже не удается.
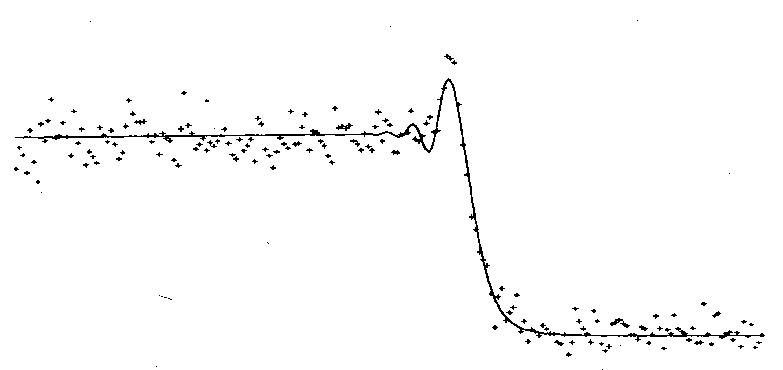
(Рис. 1 Фотоэлектрическая кривая покрытия Луной холодной углеродной звезды Y Тельца.)
Особо интересные результаты можно получить при наблюдениях покрытий Луной звезд сложной структуры в различных участках спектра их излучения (как говорят, в различных спектральных полосах). Например, автором этой статьи была получена фотоэлектрическая кривая покрытия Луной холодной углеродной звезды Y Тельца. Холодной — значит, температура ее поверхности не превышает 3000-4000 градусов Кельвина. Углеродной — значит, в спектре звезды имеются линии и полосы, вызванные присутствием в ее атмосфере углерода или некоторых его соединений. Наблюдение проводилось в Высокогорной (высота — около 3000 м над уровнем моря) Тянь-Шаньской обсерватории ГАИШ близ Алма-Аты с телескопом-рефлектором диаметром 48 см. Регистрация кривой покрытия выполнена в «красной» области оптического диапазона спектра, т.е. в спектральной полосе со средней длиной волны 7000 A(полоса «R»). Эта кривая представлена на рис. 1. Крестиками изображены данные наблюдений — отсчеты фотоэлектрического фотометра, соответствующие времени накопления 0.002 с. Сплошной линией показана теоретическая дифракционная кривая, наилучшим образом совпадающая с зарегистрированными изменениями светового потока. В результате обработки данных было получено значение углового диаметра звезды d = 0.0056±0.0012 угл. секунды.
Звезда Y Тельца является мощным источником инфракрасного излучения. Группой американских астрофизиков во главе с проф. С. Риджвэем было выполнено несколько наблюдений покрытий этой звезды Луной в ближнем инфракрасном диапазоне спектра на длинах волн 1.6-2.2 микрона (1 микрон = 10 -6 м = 10000 А). Сравнение результатов показало, что приведенная выше величина углового диаметра, найденная автором, заметно меньше (примерно в полтора раза), чем значения, полученные из анализа инфракрасных наблюдений. Как объяснить такое расхождение?
Можно высказать по этому поводу как минимум два предположения. Первое: звезда Y Тельца пульсирует, ее диаметр меняется со временем в значительных пределах. Такие пульсации — довольно типичное явление у гигантских холодных («красных») звезд. Пульсирует красный сверхгигант Антарес, пульсирует с большой амплитудой ярчайшая красная звезда в созвездии Ориона — Бетельгейзе. Пульсации могут происходить строго периодически, но могут и не иметь определенного постоянного периода, например, быть, как говорят, квазипериодическими («как бы» периодическими). Если сопоставить имеющиеся данные измерений углового диаметра Y Тельца с фазами переменности блеска звезды (эта давно известная переменность не является строго периодической, но все же некоторое среднее значение периода повторений одного и того же уровня блеска было выведено из многолетних наблюдений), то, как будто, намечается такая зависимость, при которой меньшее значение углового (а значит, и линейного) диаметра звезды соответствует более высокой яркости (а значит, светимости), и наоборот. Подобное поведение напоминает пульсации цефеид, у которых сжатие звезды сопровождается увеличением ее температуры и светимости, а при расширении, наоборот, светимость падает. К сожалению, гипотезу о пульсациях звезды Y Тельца пока трудно подтвердить или опровергнуть, т.к. имеющихся данных измерений углового диаметра еще недостаточно для этого.
Второе предположение: звезда Y Тельца окружена пылевой оболочкой или протяженной атмосферой (на это указывают также данные исследования излучения звезды в различных участках спектра), и оптическое излучение основного тела звезды, выходящее с поверхности ее фотосферы, проходит сквозь эту газопылевую околозвездную оболочку, отдавая некоторую часть своей энергии ее частицам; энергия, поглощенная в атмосфере и (или) оболочке, переизлучается в космическое пространство на б`ольших длинах волн, т.е. в ближнем инфракрасном диапазоне; в результате мы можем наблюдать излучение фотосферы в оптическом диапазоне и одновременно регистрировать инфракрасное излучение от оболочки (атмосферы), которая имеет гораздо большие размеры. Если принять такое предположение, то кривая покрытия, полученная при наблюдении в оптическом диапазоне, должна соответствовать угловому диаметру фотосферы звезды, а кривые, полученные в ближнем ИК-диапазоне, — наиболее интенсивно излучающим в этой области спектра слоям газопылевой оболочки. В рамках этого предположения, используя оценку расстояния до звезды (около 520 парсек), можно оценить линейные диаметры фотосферы 630 Rc (Rc = 
км — радиус Солнца) и излучающего слоя оболочки 970 Rc. Анализ данных о потоках излучения от звезды на разных длинах волн позволяет заключить, что температура на уровне фотосферы, по-видимому, близка к 2700-2800 К, а температура, характеризующая излучение пылевой оболочки или протяженной атмосферы, вероятно, составляет около 2000-2300 К; при этом вклад газопылевой оболочки в интегральное излучение звезды (на всех длинах волн) может достигать 30-50%. Некоторая осторожность, с которой высказано последнее утверждение, и соответствующие оговорки связаны с тем, что уверенное определение указанных величин представляет собой весьма сложную задачу, требующую отдельного рассмотрения.
Огромные размеры звезды Y Тельца означают, что она принадлежит к классу сверхгигантов. Вполне возможно, что в действительности результаты измерений ее углового диаметра отражают и реальные изменения ее размеров, и влияние газопылевой оболочки. Вероятно, истинная картина прояснится по мере накопления данных наблюдений.
Таковы в общих чертах широкие возможности использования в астрономии метода наблюдений покрытий звезд Луной. Это один из ярких примеров того, как эффективно человек может использовать явления и процессы, существующие в природе, для исследования самой природы. Нужно только увидеть и оценить эти ее «подарки».
Источник