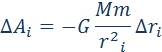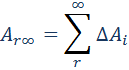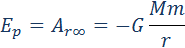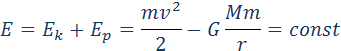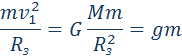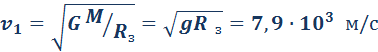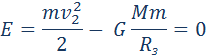ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Вопросы к экзамену
Для всех групп технического профиля

Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»
Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
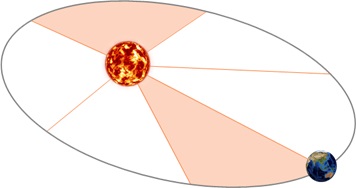
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
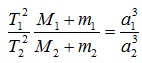
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 — соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:
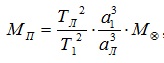
где Тл и α л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
б) для внутренней планеты:
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Источник
Задача кеплера луна земля
Современная формулировка первого закона дополнена так: в невозмущенном движении орбита движущегося тела есть кривая второго порядка – эллипс, парабола или гипербола.
В отличие от двух первых, третий закон Кеплера применим только к эллиптическим орбитам.
Скорость движения планеты в перигелии
где v c – средняя или круговая скорость планеты при r = a . Скорость движения в афелии
Кеплер открыл свои законы эмпирическим путем. Ньютон вывел законы Кеплера из закона всемирного тяготения . Для определения масс небесных тел важное значение имеет обобщение Ньютоном третьего закона Кеплера на любые системы обращающихся тел.
Комета Галлея обращается вокруг Солнца с периодом обращения 76 лет. Нептун имеет период обращения 164,8 лет. Кто из них более удален от Солнца в точке афелия своей орбиты?
аГ = 17,8 а.е., q = 0,59 а.е. Комета удаляется от Солнца на 2∙17,8 – 0,59 = 35,01 а.е.
Большая полуось Нептуна а Нептуна = 30 а.е.
Ответ. Дальше от Солнца в афелии находится комета Галлея.
Комета Темпеля имеет вытянутую орбиту, ее перигелийное расстояние 1,37 а.е., период обращения вокруг Солнца Т = 5,26 лет. Найти наибольшее расстояние от Солнца, большую полуось и эксцентриситет кометы Темпеля.
Большую полуось можно найти из третьего закона Кеплера T 2 / T 2 = a 3 / a 3 ;
где Т = 1 год, а = 1 а.е.
Наибольшее расстояние от Солнца – афелий орбиты кометы Q = 2 a – q = 4,63 а.е.
Ответ. Эксцентриситет е = 0,54, афелий Q = 4,63 а.е., большая полуось а = 3,0 а.е.
В XVIII веке была подмечена закономерность, которая в настоящее время называется правилом Тициуса–Боде. Средние расстояния от планет до Солнца выражаются, согласно этому правилу следующей формулой: а = 0,1∙(3∙2 n + 4) а.е.
В 1993 году у пульсара PSR В 1257+12 были найдены три планеты. Все они находятся на расстояниях, пропорциональных (но не равных) расстояниям от Солнца Меркурия, Венеры и Земли (0,30/0,72/1,0). Что изменится в формулировке правила Тициуса – Боде для данной системы? Ответ. Коэффициент перед скобкой.
Замечено, что противостояния некоторой малой планеты повторяются через 2 года. Чему равна большая полуось ее орбиты?
Понятие противостояния определено только для внешних планет:
сидерический период Т = 2 года, а по третьему закону Кеплера T 2 / T 2 = a 2 / a 2 , отсюда большая полуось орбиты а = 1,59 а.е. Внешняя планета находится за орбитой Марса.
Сколько времени нужно лететь с Земли на Марс по гомановской орбите в космическом корабле, перигелийное расстояние которого равно расстоянию от Земли до Солнца, а афелийное расстояние – расстоянию от Марса до Солнца?
По третьему закону Кеплера
большая полуось орбиты космического корабля
Для Земли T = 1 год, a = 1 а.е., поэтому T = 1,4 года, а время полета
Контрольная работа. Конфигурации планет. Законы Кеплера. Вариант № 1
Какие небесные явления происходят при данных конфигурациях небесных тел:
1. Если А — планета Марс; В — Земля; С — Солнце, произойдет:
1) солнечное затмение; 2) лунное затмение; 3) противостояние; 4) верхнее соединение; 5) нижнее соединение; 6) покрытие.
2. Если А — Земля; В — Солнце; С — планета Венера, произойдет:
1) солнечное затмение; 2) лунное затмение; 3) противостояние;
4) верхнее соединение; 5) нижнее соединение; 6) покрытие.
3. В нижнем соединении не могут находиться … планеты:
1) внешние; 2) внутренние; 3) нижние планеты.
4. Рядом с Луной во время полнолуния могут быть видны … планеты:
1) только внутренние; 2) только внешние; 3) как внутренние, так и внешние; 4) во время полнолуния рядом с Луной планеты нельзя наблюдать.
5. Максимальное угловое отклонение от Солнца наблюдается у:
1) Венеры; 2) Меркурия; 3) Марса.
6. Как меняется значение скорости движения кометы при ее перемещении от перигелия к афелию?
1) не изменяется; 2) увеличивается; 3) уменьшается; 4) скорость кометы не зависит от положения на орбите.
7. По каким траекториям движутся космические аппараты к Луне от Земли?
1) по параболе; 2) по эллипсу, в одном из фокусов которого находится Земля; 3) по эллипсу, в одном из фокусов которого находится Солнце; 4) по прямой.
Контрольная работа. Конфигурации планет. Законы Кеплера. Вариант № 2
Какие небесные явления происходят при данных конфигурациях небесных тел:
1. Если А — планета Юпитер; В — Земля; С — Солнце, произойдет:
1)солнечное затмение; 2)лунное затмение; 3)верхнее соедениние; 4) противостояние; 5) нижнее соединение; 6) покрытие.
2. Если А — Земля; В — Солнце; С — планета Меркурий, произойдет:
1) солнечное затмение; 2) лунное затмение; 3) верхнее соединение; 4) противостояние; 5) нижнее соединение; 6) покрытие.
3. В нижнем соединении могут находиться … планеты:
1) внешние; 2) внутренние; 3) верхние планеты.
4. Рядом с Луной во время полного лунного затмения могут быть видны … планеты:
1) только внутренние; 2) только внешние; 3) как внутренние, так и внешние; 4) во время полнолуния рядом с Луной планеты нельзя наблюдать.
5. Максимальное угловое отклонение от Солнца наблюдается у:
1) Венеры; 2) Меркурия; 3) Юпитера.
6. Как меняется сидерический период обращения планет-гигантов вокруг Солнца с удалением от него?
1) Чем дальше планета от Солнца, тем ее сидерический период больше.
2) Чем дальше планета от Солнца, тем ее сидерический период меньше.
3) Период обращения планет-гигантов не зависит от их расстояния до Солнца.
4) Период обращения планет-гигантов вокруг Солнца равен периоду их обращения вокруг оси.
7. По каким траекториям движутся космические аппараты к Луне от Земли?
1) по параболе; 2) по эллипсу, в одном из фокусов которого находится Земля; 3) по эллипсу, в одном из фокусов которого находится Солнце; 4) по прямой.
Источник
Законы Кеплера
В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.
Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.
Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации – открытию закона всемирного тяготения.
С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям (рис. 1.24.1). Первая попытка создания модели Вселенной была предпринята Птолемеем (
140 г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.
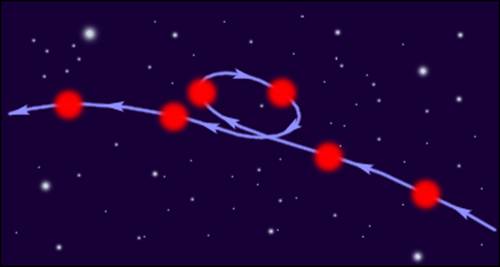 |
| Рисунок 1.24.1. Условное изображение наблюдаемого движения Марса на фоне неподвижных звезд |
Геоцентрическая система Птолемея продержалась более 14 столетий и только в середине XVI века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми. Немецкий астроном Иоганн Кеплер в начале XVII века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы. Кеплер использовал результаты наблюдений за движением планет датского астронома Тихо Браге.
Первый закон Кеплера (1609 г.):
Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
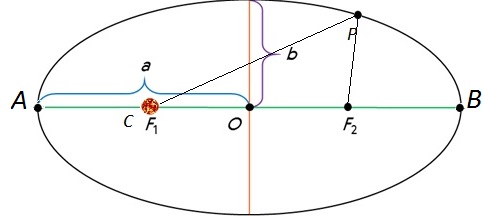
На рис. 1.24.2 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка P траектории называется перигелием, точка A, наиболее удаленная от Солнца – афелием. Расстояние между афелием и перигелием – большая ось эллипса.
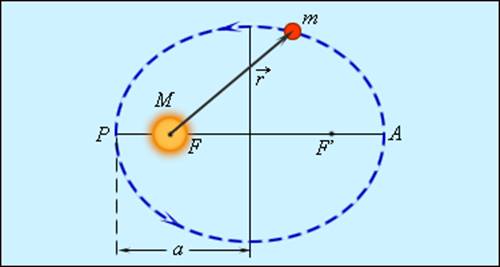 | ||||
| Рисунок 1.24.2. Эллиптическая орбита планеты массой m –11 Н·м 2 /кг 2 – гравитационная постоянная. Ньютон первый высказал мысль о том, что гравитационные силы определяют не только движение планет Солнечной системы; они действуют между любыми телами Вселенной. В частности, уже говорилось, что сила тяжести, действующая на тела вблизи поверхности Земли, имеет гравитационную природу. Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что T 2 R 3 , где Т – период обращения, R – радиус орбиты. Отсюда можно получить зависимость гравитационной силы от расстояния. При движении планеты по круговой траектории на нее действует сила, которая возникает за счет гравитационного взаимодействия планеты и Солнца: Свойство консервативности гравитационных сил позволяет ввести понятие потенциальной энергии. Для сил всемирного тяготения удобно потенциальную энергию отсчитывать от бесконечно удаленной точки. Потенциальная энергия тела массы m, находящегося на расстоянии r от неподвижного тела массы M, равна работе гравитационных сил при перемещении массы m из данной точки в бесконечность. Математическая процедура вычисления потенциальной энергии тела в гравитационном поле состоит в суммировании работ на малых перемещениях (рис. 1.24.5).
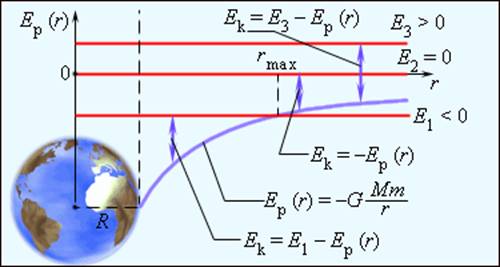
Закон всемирного тяготения применим не только к точеным массам, но и к сферически симметричным телам. Работа Полная работа при перемещении тела массой m из начального положения в бесконечность находится суммированием работ ΔAi на малых перемещениях: В пределе при Δri → 0 эта сумма переходит в интеграл. В результате вычислений для потенциальной энергии получается выражение Знак «минус» указывает на то, что гравитационные силы являются силами притяжения. Если тело находится в гравитационном поле на некотором расстоянии r от центра тяготения и имеет некоторую скорость υ, его полная механическая энергия равна В соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной. Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела (рис. 1.24.6). При E = E1 rmax. В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы).
При E = E2 = 0 тело может удалиться на бесконечность. Скорость тела на бесконечности будет равна нулю. Тело движется по параболической траектории. При E = E3 > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии. Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля. Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли. Эту скорость необходимо набрать, чтобы преодолеть притяжение Земли и вывести тело (например, спутник) на орбиту Земли. Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории. Рис. 1.24.7 иллюстрирует космические скорости. Если скорость космического корабля равна υ1 = 7.9·10 3 м/с и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих υ1, но меньших υ2 = 11,2·10 3 м/с, орбита корабля будет эллиптической. При начальной скорости υ2 корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе. Источник ➤ Adblockdetector |
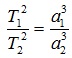
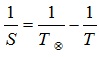
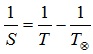






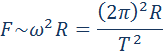
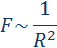
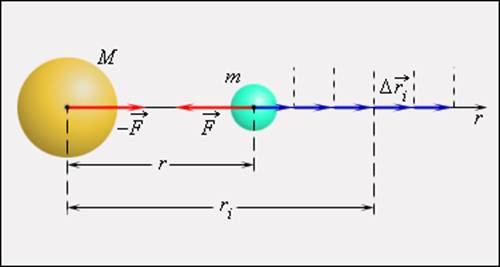
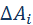 гравитационной силы
гравитационной силы 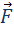 на малом перемещении
на малом перемещении 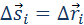 есть:
есть: