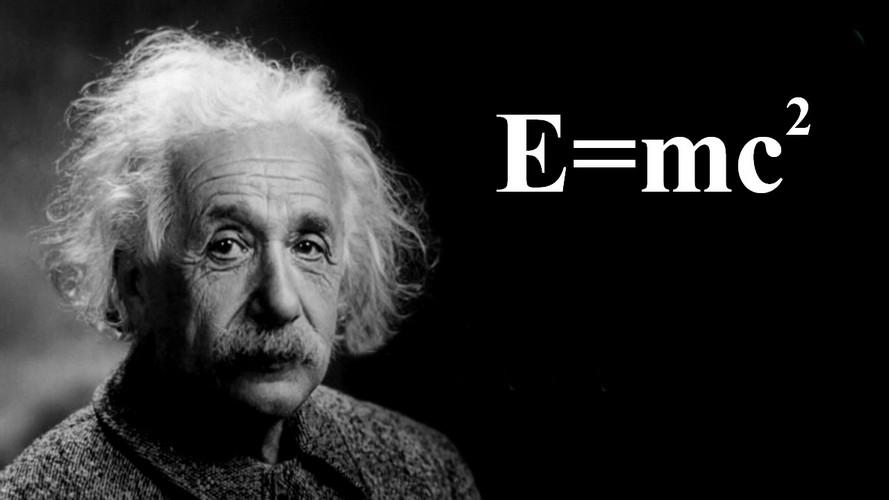Закон ньютона все тела во вселенной

Поскольку слоев бесконечно много, то и света должно быть бесконечно много. Ночью должно быть светло, как днем — вот о чем говорит парадокс Ольберса.

Что же делать? Опять ждать гения? Но может быть, стоит и самим чуточку подумать?

Исходные посылки: Вселенная бесконечна, изотропна, однородна и постоянна.
Изотропность и однородность установлены точно и здесь ничего изменить нельзя.

Делаем вывод, что либо Вселенная не бесконечна, либо Вселенная изменяется со временем.

И здесь на помощь приходит еще один гений — американский астроном Хаббл

В 1929 г. Хаббл измерял скорости движения галактик. Для этого он определял так называемое “красное смещение” — наблюдаемый в спектрах излучения галактик сдвиг спектральных линий, присущих определенным химическим элементам, в сторону более длинных волн по сравнению с их нормальными.
И он получил следующую картину:

Скорость (v) удаления галактик в зависимости от их расстояния (R) от нашей Галактики описывается простым выражением (Э. Хаббл, 1929)
v=HR

Постоянная Н называется постоянной Хаббла и ее современное значение составляет около 70 км/с Мпк.

Наблюдаемое Хабблом красное смещение означает, что объект удаляется от наблюдателя.

Итак, существующая Вселенная нестационарна, галактики убегают от нас.

Ура (ликуют все жители Земли), значит, Земля (точнее, наша галактика) является центром Вселенной?

Ликование было недолгим, потому что опять вмешивается наш разум и приводит простую аналогию с воздушным шариком.

Будем надувать воздушный шарик с нарисованными на нем точками 1, 2, 3.

Происходит “разбегание” точек 1, 2 и 3 по поверхности шара при увеличении его размеров.

Так и во Вселенной. Все галактики разбегаются друг от друга, и конечно, возникает вопрос, почему?

На помощь снова приходит гениальный ученый – теперь это русский ученый Фридман

В начале 20-х годов он предложил модель нестационарной Вселенной.

Если сейчас галактики разбегаются, то вчера они были ближе, а позавчера еще ближе друг к другу, а значит был момент времени t=0, когда все началось из какой-то точки. Обратите внимание, что здесь самое главное – это временная шкала, мы приходим к выводу о моменте рождения Вселенной.

Конечно, мы получаем также свидетельство, что Вселенная была в точке (в математическом смысле, а вспомните, что есть точка в математике?), но реально никакой точки не было.

Но почему галактики разбегаются. Предположим, что в начальный момент времени уже были галактики и занимали какое-то пространство.

Предположим также, что в начальный момент галактики были в покое, т.е. их скорость v=0. Тогда галактики будут притягиваются друг к другу и Вселенная будет сжиматься.
Но если в начальный момент скорости были большими и направлены таким образом, что галактики удалялись друг от друга, то мы получим, что и в настоящее время галактики удаляются друг от друга (правда, с меньшей скоростью, поскольку тяготение «тормозит» их движение).
Время рождения Вселенной грубо можно оценить из закона Хаббла: зная расстояние между галактиками и скорость их расхождения, можно из S=vt найти время t. После введения поправок на замедление расширения получаем время рождения Вселенной — примерно 15 млрд лет тому назад.
Итак, был начальный момент, когда произошел «Большой Взрыв»

(Детский вопросик – Что, где и когда взорвалось?)

Иными словами, после «взрыва» частицы получают огромную начальную скорость и начинают разлетаться во все стороны. Если силы притяжения, которые стремятся собрать частицы воедино, малы, то частицы все время будут разлетаться. Однако если силы притяжения велики, то через некоторое время они изменят знак скорости движения частиц на противоположный и частицы начнут сближаться. Ясно, что гравитационные силы зависят от плотности частиц в объеме Вселенной — чем больше плотность, тем больше силы F тяг . Из приведенных условий ясно, что сценарий развития Вселенной зависит от плотности вещества в современную эпоху, т.е. существует критическая величина плотности r Вселенной. Открытая модель соответствует r r кр . Обратное неравенство справедливо для закрытой модели. По современным данным, критическая плотность вещества составляет r кр = 5х10 -30 г/см 3 . Примерно такое же значение дают оценки плотности вещества во Вселенной.
Изменение размера R Вселенной с течением времени t для Вселенной с разной плотностью.

Строгое решение задачи об эволюции (развитии) Вселенной показывает:

Неужели все так просто и ясно? Что же еще ученым надо, и что они делали после этого еще 70 лет?
Однако в последнее время появились новые астрономические данные, проливающие свет на современное состояние Вселенной и на ее будущее. Подробнее см. тему 5.

Спасибо, что осилили сложную тему.
Мне кажется, что теперь вы в состоянии создать такую фигуру:

Источник

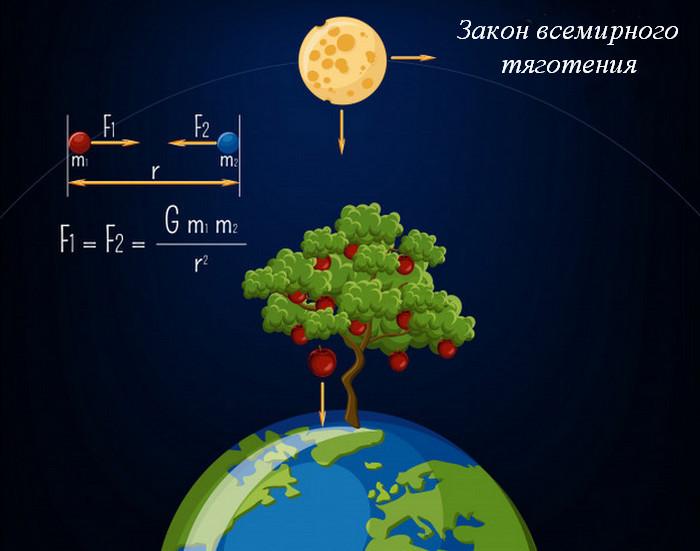
Определение и вывод закона всемирного тяготения

Тяготение – привычное явление для каждого живого существа на Земле, на первый взгляд, не требующее объяснений. Описывает это явление закон всемирного тяготения. Однако стоит углубиться в данную тему чуть больше, так сразу возникает ряд вопросов, для ответа на которые потребуются постулаты классической механики Ньютона, а также теории относительности и базирующейся на ней теории квантовой гравитации.

Что такое всемирное тяготение

Земля — это большой магнит, который притягивает к себе всё, что находится рядом: и карандаш, случайно выскользнувший из пальцев рук, и астероид, пролетающий мимо. С начала развития науки учёные давали своё видение и определение явлению всемирного тяготения, но только в 1687 году в фундаментальной работе Исаака Ньютона «Математические начала натуральной философии» было доказано его существование и воздействие на окружающие объекты.

Основываясь на известные к тому времени эмпирические соотношения Иоганна Кеплера, описывающие гелиоцентрическую картину мира, Ньютон определил закон, согласно которому все тела притягиваются друг к другу.

Причём сила взаимодействия растёт с увеличением массы и в то же время связана с расстоянием между объектами обратной квадратичной зависимостью, т.е.:

Несмотря на то, что объектами относительно небольшой массы данное явление практически не воспринимается, именно гравитация управляет движением астрономических тел, а формулировка закона позволяет объяснить, почему планеты движутся вокруг Солнца, а Луна – вокруг Земли.

Природа силы всемирного тяготения

Если важная роль гравитации в работе Вселенной понятна и неоспорима, то дать чёткий ответ на вопрос, откуда эта сила появляется, гораздо сложнее. В первой половине XX века Альберт Эйнштейн предложил специальную и общую теории относительности, в которых раскрыл своё видение природы всемирного тяготения. Согласно учёному, пространство и время представляют собой пространственно-временной континуум – четырёхмерное пространство, одно из измерений которого – время. Но так как люди воспринимают окружающее их пространство и течение времени в отдельности друг от друга, то они видят лишь проекцию континуума. Эйнштейн предположил, что гравитация возникает вследствие того, что тела, обладающие массой, вызывают деформацию пространства при проецировании на него четырёхмерного континуума.

Более понятной идея учёного будет выглядеть, если проиллюстрировать её с помощью двух шаров разной массы и обычного листа бумаги. Допустим, что лист держат за края в горизонтальном положении, а в его центр помещают один из шаров, более тяжёлый. Естественно, бумага прогнётся. Покатив по прямой линии лёгкий шарик, наблюдатель обнаружит, что его траектория является дугообразной, стремящейся к первому, более тяжёлому шару. Причём, с позиции шара меньшей массы, его движение продолжает быть прямолинейным. В этой иллюстрации и заключено упрощённое видение возникновения гравитации как явления.

История открытия закона всемирного тяготения

Существует легенда, согласно которой Ньютон, прогуливаясь по саду и наблюдая за луной, увидел, как падает на землю яблоко (в другой версии, это яблоко упало на голову учёного). В этот же момент он подумал, что, есть вероятность, что одна и та же сила удерживает спутник на небе и заставляет фрукты падать с веток деревьев. Эта догадка и послужила началом работы над законом притяжения.

Сегодня историки сомневаются в этом мифе, что вполне объяснимо, однако главным фактом в истории остаётся то, что Ньютон был первым учёным, который осознал, что тела на Земле и в космосе испытывают на себе воздействие одной и той же силы. До этого момента люди делили гравитацию на два типа: первый отвечал за земное, несовершенное взаимодействие, второй – за небесное, заставляющее планеты двигаться по круговым, совершенным, траекториям.

Ньютон математически связал гравитацию и соотношения движения планет, выведенные Кеплером, прекращая тем самым ложное разделение физических устоев Земли и остальной Вселенной.

Вывод закона всемирного тяготения

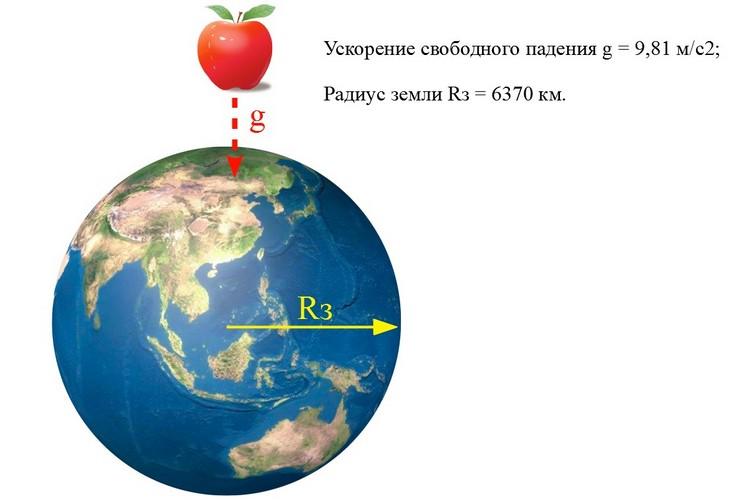
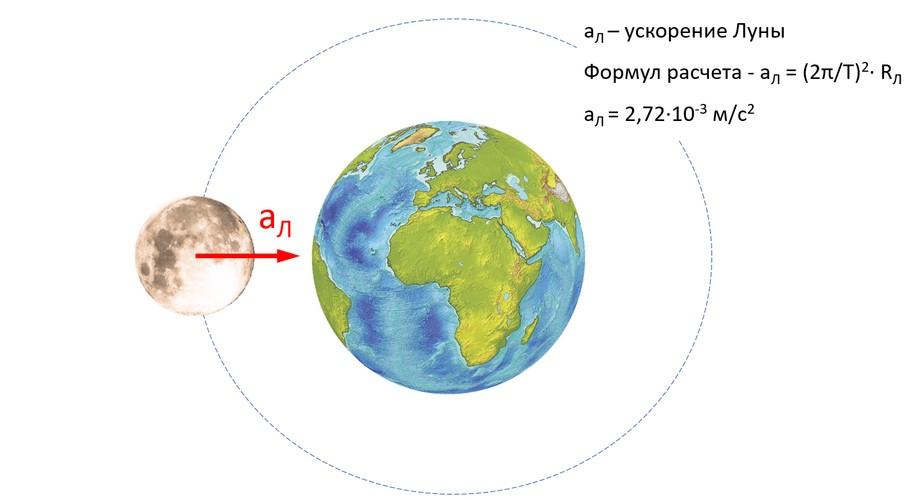
Исаак Ньютон описал свою математическую модель гравитационного воздействия, рассматривая движение Луны вокруг Земли.

Притяжение тел к земле

Известно, что радиус Земли составляет R_З = 6370 километров, а всякий объект на её поверхности, обладает ускорением свободного падения g = 9,81 м/с 2 .

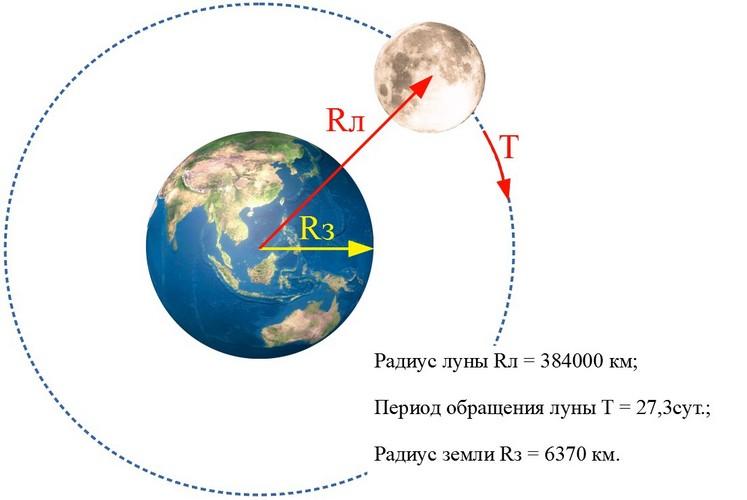
Притяжение Земли и Луны

Известно, что Луна вращается вокруг Земли, двигаясь по круговой орбите радиусом R_Л = 384000 километров, период обращения при этом равен T = 27,3 суток. Для того чтобы численно прикинуть, насколько орбита Луны больше радиуса Земли, требуется разделить имеющиеся величины друг на друга, то есть:

По полученным результатам очевидно, что путь от планеты до спутника включает в себя 60 радиусов Земли.

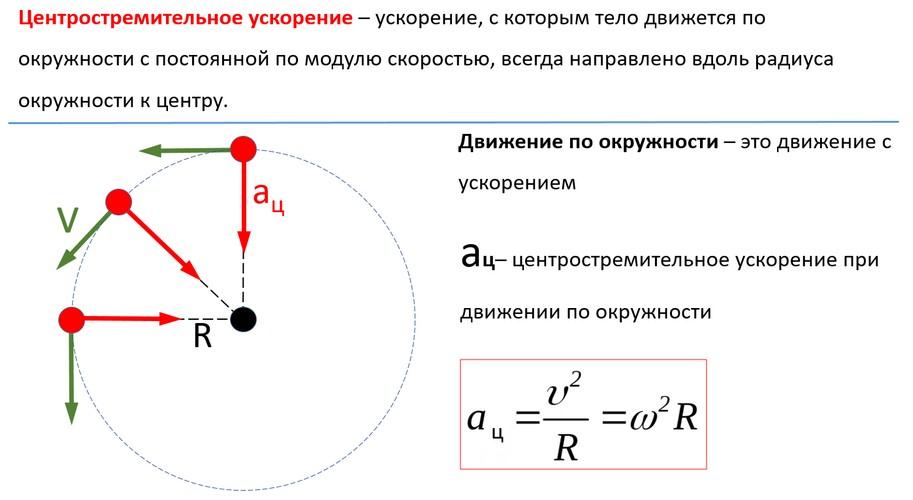
Ускорение в формуле всемирного тяготения

Луна притягивается к ней с ускорением, которое называют центростремительным. Известно, что центростремительное ускорение находят по формуле:

где ω – угловая скорость движения;

R – радиус окружности, по которой происходит движение.

Угловая скорость ω и период обращения Т связаны между собой соотношением:

Подставляя это равенство в формулу ускорения и преобразуя её путём подстановки индексов к некоторым величинам, получаем:

где a_Л – ускорение Луны;

R_Л – орбита Луны или расстояние от неё до Земли.

Перед тем, как получить численное значение искомого ускорения, требуется перевести размерности всех компонентов в соответствии с Международной системой единиц (СИ):

• период Т = 27,3 суток = 655,2 часа = 39312 минут = 2358720 секунд;
• расстояние R = 384000 километров = 384 ∙10 6 метров.

Таким образом, спутник движется с ускорением:

a_Л = (2∙3,14 / 2358720) 2 ∙ 384 ∙10 6 = 2,72∙10 -3 м/с 2 .

Сравнивая полученную величину со значением g, получаем:

g/ a_Л = 9,81 / 2,72∙10 -3 ≈ 3600 = 60 2 .

То есть ускорение, получаемое на орбите Луны, в 60 2 раз меньше ускорения, которое приобретается на поверхности Земли, при этом спутник находится в 60 раз дальше, то есть напрашивается предположение, согласно которому ускорение обратно пропорционально значению расстояния, возведённому в квадрат:

Второй и третий законы Ньютона в выводе формулы тяготения

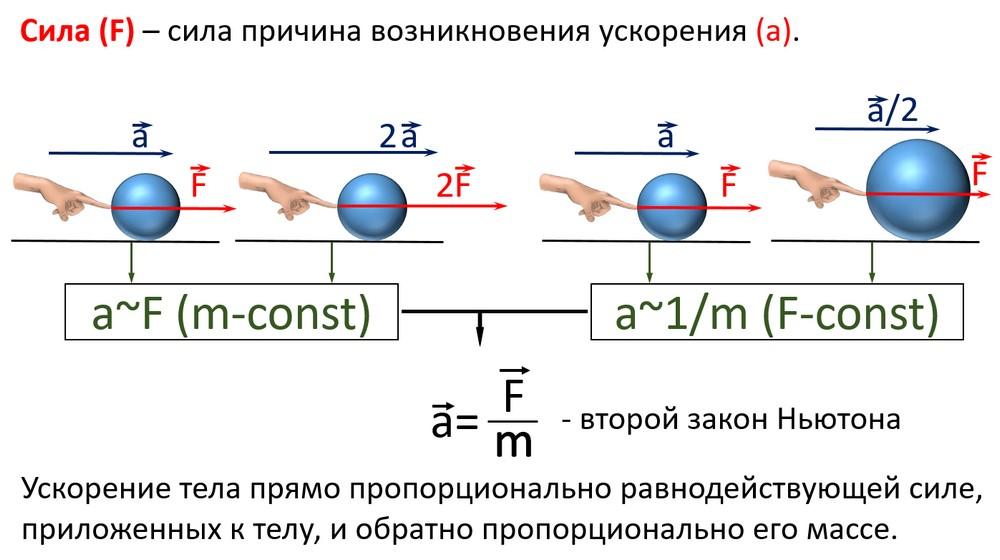
Второй закон Ньютона утверждает, что ускорение a, которое получает тело, прямо пропорционально зависит от равнодействующей сил F, которые приложены к этому телу, и находится в обратной зависимости от его массы m:

Исходя из этого, напрашивается утверждение, что характер приращения силы идентичен характеру приращения ускорения, то есть:

А так как уже было выдвинуто предположение, что ускорение имеет обратно пропорциональную зависимость от квадрата расстояния, то у силы, действующей на тело, такой же характер, то есть:

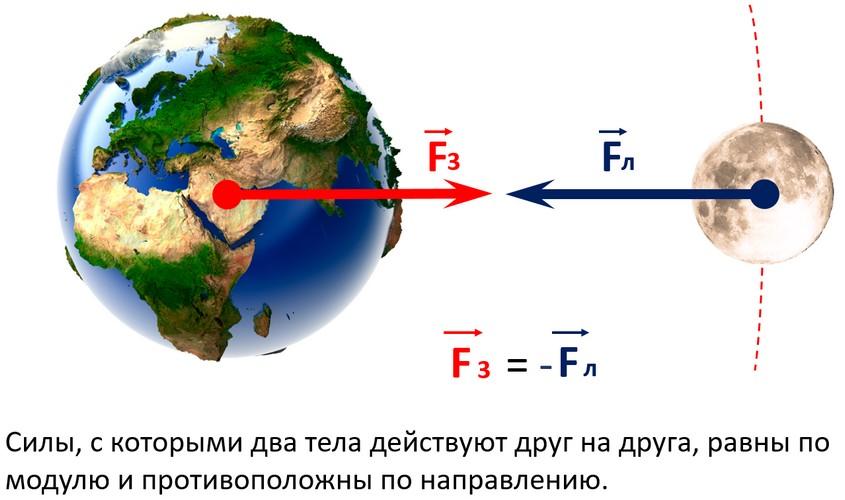
В это же время известно, что по третьему закону Ньютона взаимодействие тел между собой становится причиной возникновения сил, направленных в противоположные стороны, но одинаковых по модулю:

где F₁₂ – сила, с которой первое тело воздействует на второе;

F₂₁ – сила, действия второго тела на первое.

Таким образом, не только Земля притягивает к себе свой спутник, но и наоборот. А так как по второму закону Ньютона приращение силы прямо зависит не только от приращения ускорения, но и массы, то можно утверждать, что притяжение между Луной и Землёй соответствует записи:

где m_Л – масса Луны;

Знак умножения здесь получен в результате конъюнкции – логической операции, синонимами которой являются «логическое умножение» и «И» (потому что на притяжение влияет и масса Луны, и масса Земли).

Формула всемирного тяготения

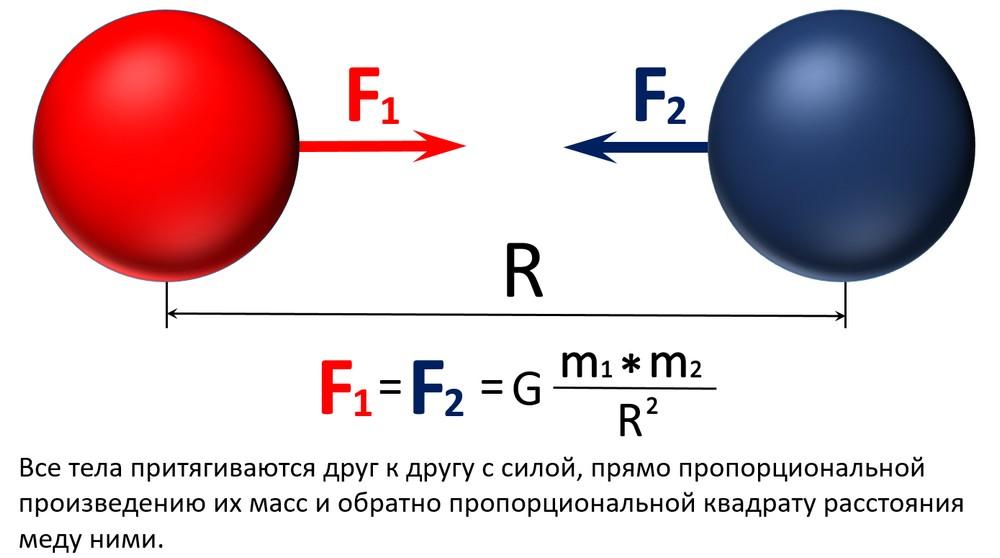
Суммируя полученные вычисления и предположения, можно вывести запись:

Но так как данное соотношение действует не только на нашу планету и её спутник, а на все объекты, то полученный вид следует слегка преобразовать:

где F – сила притяжения, возникающая при взаимодействии двух тел;

m_1,2 – масса первого и второго тела;

Для того чтобы пропорциональность стала равенством, требуется специальный коэффициент G, называемый гравитационной постоянной. После его введения итог совершённых преобразований получает название формулы закона всемирного тяготения:

В чём измеряется сила притяжения

В СИ размерность любой силы — это ньютоны (Н), следовательно, сила притяжения измеряется в тех же величинах. Ньютоны считаются производными единицами, которые формируются установленными основными. Таким образом, ньютон это отношение килограмма (кг) к отношению метра (м) на секунду в квадрате (с 2 ), то есть Н = кг / (м/с 2 ) .

Гравитационная постоянная

Значение постоянной G приравнивается силе притяжения двух точечных тел, обладающих массой один килограмм и расположенных в одном метре. Согласно СИ,

G = 6,67∙10 -11 Н∙м²·кг −2 .

Опыт Кавендиша

Чтобы определить гравитационную постоянную, был проведён эксперимент, где главную роль играли крутильные весы – устройства, представляющего собой прочную стальную проволоку, на которой расположено горизонтальное коромысло, утяжелённое по краям двумя одинаковыми шарами из свинца. Масса каждого составляла 730 грамм.

В ходе эксперимента Кавендиш приближал к маленьким шарикам большие, весом 158 килограмм, подвешенные также на коромысле. При подведении тяжёлых шаров возникала сила взаимного притяжения, поворачивающая коромысло и закручивающая проволоку, что вызывало появление силы упругости, противодействующей притяжению шаров. В определённый момент сила гравитационного взаимодействия уравновешивалась с силой упругости закрученной проволоки. Регистрируя оптическими устройствами отклонения шаров и сравнивая силы, действующие на систему, Кавендиш вычислил значение коэффициента.

Инфографика-вывод закона всемирного тяготения

Сила тяжести как частный случай закона всемирного тяготения

Создав математическую модель притяжения, Ньютон установил, что сила тяжести, чьё влияние видел и испытывал на себе каждый, является лишь одним из проявлений всемирного тяготения, которое утверждает, что все тела во Вселенной, включая планеты, звёзды, астероиды и т.д., воздействуют друг на друга с определённой силой.

Чтобы узнать значение этой силы, исходящей от Земли, нужно воспользоваться формулой, выражающей прямо пропорциональную зависимость воздействия и массы объекта:

На поверхности значение ускорения свободного падения принимают равным 9,81 м/с 2 . Если же тело удалено от поверхности Земли, значение g можно найти по формуле:

где h – расстояние до земли.

Таким образом, действие силы тяжести на тело уменьшается с увеличением высоты.

Интересный факт: если принять силу тяжести, действующую на Земле, за единицу, то можно проанализировать значение притяжения на поверхности других небесных тел. Так, самое большое воздествие тяготения испытает на себе тело на поверхности Юпитера – 2,442, а самое маленькое – на Луне (0,165).

В каких случаях справедлив закон всемирного тяготения

Выявленная Ньютоном зависимость имеет ограничения в области применения. Так, закон справедлив только в случаях, когда:

1. тела можно принять материальными точками, то есть их размеры настолько малы по отношению к расстоянию, что ими можно пренебречь;
2. тела обладают сферической формой, что свидетельствует об однородном распределении массы внутри них;
3. одно из тел – шар большого диаметра, а второе имеет несопоставимо маленькие размеры.

Соотношение неприменимо, если требуется описать взаимодействие шара и стержня бесконечной длины. В этом случае сила притяжения будет пропорциональна не квадрату расстоянию, а его модулю. А если существует потребность определить тяготение между бесконечной плоскостью и телом, расстояние вообще не будет иметь влияния.

Применение закона всемирного тяготения

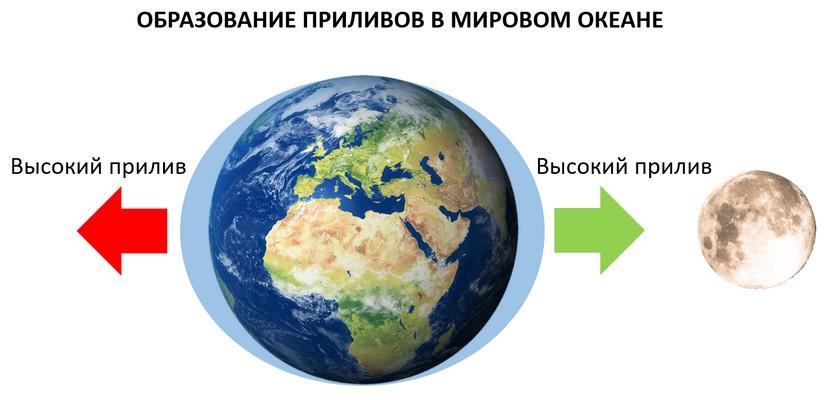
Закон всемирного тяготения – это фундаментальный закон механики, после формулировки которого стало возможно объяснение и предсказание множества природных явлений. К ним относятся:

• приливы и отливы;
• точное время и место лунных и солнечных затмений;
• масса Солнца и других астрономических тел;
• орбиты движения планет и их спутников.

Открытие планет с использованием закона всемирного тяготения

После открытия явления притяжения астрономы и физики могли, опираясь на закон Ньютона и соотношения Кеплера, определять траектории движения наблюдаемых планет Солнечной системы и указывать их координаты в любой момент времени, причём правильность вычислений подтверждалась эмпирически – результатами астрономических наблюдений.

В 1781 году Уильямом Гершелем была открыта седьмая планета Солнечной системы – Уран. Следуя отработанному алгоритму, астроном рассчитал траекторию своего открытия и его орбиту, однако в первой половине XIX века учёные обнаружили несоответствие вычисленных и реальных координат. Возникло предположение, что, помимо Солнца и шести других планет, на Уран воздействует ещё одна планета, находящаяся за ним.

В 1846 году ночью 23 сентября на основании теоретических расчётов, выполненных по имеющимся отклонениям Урана от рассчитанной траектории, молодым сотрудником Британской обсерватории Иоганном Галле была обнаружена предсказанная планета, названная Нептуном.

Интересный факт: расчёты, после проведения которых стало возможно открытие, в одно и то же время совершили два учёных, независимо друг от друга – Джон Адамс и Урбен Леверье.

Спустя практически 100 лет, 18 февраля 1930 года, подобным образом была открыта девятая планета – Плутон, которая из-за относительно небольших размеров и массы считается карликовой.

Закон всемирного тяготения. Примеры из жизни

Притяжение испытывает на себе любой объект во Вселенной. В обычной жизни действие этого закона можно наблюдать в каждом явлении падения тел с высоты, будь то листок с дерева, камень, капли дождя, горные обвалы и оползни.

Кроме этого, тяготение проявляется в наличии веса у каждого объекта – силы, с которой тело воздействует на опору, препятствующую его дальнейшему падению к центру Земли.

Границы применимости

Несмотря на то, что закон всемирного тяготения Ньютона объясняет работу множества явлений, в конце XIX века было выявлено несоответствие наблюдаемого и рассчитанного смещения перигелия Меркурия. Эта особенность движения планеты не объяснялась известным законом, что потребовало новое понимание гравитации.

Кроме того, на рубеже веков применимость классической механики, основанной на законах Ньютона, подверглась ограничениям. Получение точных результатов с её помощью возможно только в случаях, когда:

• скорость тел гораздо меньше скорости звука;
• размеры объектов гораздо больше размеров атомов и молекул;
• скорость распространения гравитации считается бесконечной.

Дальнейшее развитие

С момента создания теории притяжения многие учёные, не разделявшие научных взглядов Ньютона, стремились усовершенствовать его закон. А возникновение трудностей XIX века, подвергших сомнению основы, потребовало внесение коррективов, которые могли бы объяснить расхождение наблюдаемого и рассчитанного. В 1915 году Альберт Эйнштейн создал общую теорию относительности (ОТО), которая объяснила смещение перигелия Меркурия и сегодня является самой перспективной теорией гравитации, доказанной множеством экспериментов.

ОТО имеет чётко выраженные границы применимости, что выражается, например, в невозможности её применения при рассмотрении квантовых эффектов. Поэтому потребовалась новая теория, в которой уже сегодня стремятся объединить теорию относительности Эйнштейна и квантовую механику. Две указанные теории основываются на различных наборах постулатов, но, несмотря на это, квантовая гравитация – одно из основных и перспективных направлений для физических исследований.

Выводы

Все тела во Вселенной взаимно притягиваются, это явление называется гравитацией. Сила притяжения, которая действует между двумя объектами, тем больше, чем больше их массы, в то же время тяготение уменьшается с увеличением расстояния.

После прочтения данной статьи ответ на вопрос, как формулируется закон всемирного тяготения, обязательно будет быстрым и правильным. Однако важно не забывать, что формула, описанная Ньютоном, справедлива только для конкретно описанных случаев.

Более того, несмотря на существование и подтверждение новых гипотез, ньютоновская механика, включая закон всемирного тяготения, является наиболее простой из существующих теорий и верно описывает природные явления в своих границах.

Источник