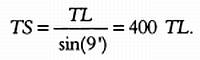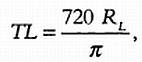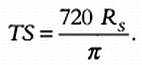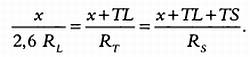Земля луна солнце треугольник

Земля луна солнце треугольник

Астрономия — это целый мир, полный прекрасных образов. Эта удивительная наука помогает найти ответы на важнейшие вопросы нашего бытия: узнать об устройстве Вселенной и ее прошлом, о Солнечной системе, о том, каким образом вращается Земля, и о многом другом. Между астрономией и математикой существует особая связь, ведь астрономические прогнозы являются результатом строгих расчетов. По сути, многие задачи астрономии стало возможным решить благодаря развитию новых разделов математики.

Из этой книги читатель узнает о том, каким образом измеряется положение небесных тел и расстояние между ними, а также об астрономических явлениях, во время которых космические объекты занимают особое положение в пространстве.

Книга: Мир математики. т.30. Музыка сфер. Астрономия и математика

Глава 2. Вычисления расстояний в системе «Земля — Луна — Солнце», выполненные Аристархом Самосским

Глава 2. Вычисления расстояний в системе «Земля — Луна — Солнце», выполненные Аристархом Самосским

Аристарх Самосский (310 год до и. э. — 230 год до н. э.) определил отношения между расстояниями и радиусами небесных тел в системе «Земля — Луна — Солнце». Он вычислил отношение между радиусом Солнца и радиусом Луны, между расстоянием от Земли до Солнца и расстоянием от Земли до Луны, а также определил отношение радиуса Земли ко всем этим расстояниям. К сожалению, исследователь не смог рассчитать значение радиуса нашей планеты и вычислить абсолютные значения всех остальных радиусов и расстояний. Радиус Земли определил Эратосфен несколько лет спустя. Применив современную нотацию (и современные значения), мы покажем, как действовал Аристарх Самосский, и предложим читателю повторить его эксперимент. Вы убедитесь, что, проведя необходимые наблюдения, нетрудно получить те же результаты, что и древний мыслитель.

Отношение расстояний между Землей и Луной и Землей и Солнцем Аристарх Самосский определил, что угол, под которым с Земли виден отрезок, соединяющий Солнце и Луну, когда Луна находится в первой четверти, равен 87°.

Сегодня мы знаем, что он допустил ошибку — возможно, потому, что определить точный момент, когда Луна находится в первой четверти, очень сложно. Реальное значение этого угла равно 89°51’, в остальном же метод Аристарха Самосского полностью корректен. Обозначим через TS расстояние от Земли до Солнца, через TL — расстояние от Земли до Луны. Так как sin (9’) = TL/TS, имеем:

Аристарх Самосский вычислил, что TS = 19 TL.

Отношение между радиусом Луны и Солнца

Отношение между радиусом Луны и Солнца должно рассчитываться по формуле, похожей на указанную выше, так как при наблюдении с Земли диаметры Луны и Солнца равны 0,5°. Следовательно, выполняется соотношение:

R_s = 400R_l.

Отношение между расстоянием от Земли до Луны и радиусом Луны или между расстоянием от Земли до Солнца и радиусом Солнца

Так как диаметр Луны при наблюдении с Земли равен 0,5°, отложив его 720 раз, можно полностью покрыть орбиту Луны (предполагается, что она имеет форму окружности). Длина ее орбиты в 2? раз больше расстояния от Земли до Луны, то есть 2R_L ? 720 = 2?TL. Выразив из этой формулы TL, имеем:

Проведя аналогичные рассуждения и предположив, что Земля вращается вокруг Солнца по окружности радиуса TS,

Отношение между расстояниями до Земли и радиусами Луны, Солнца и Земли

Во время лунного затмения Аристарх Самосский заметил, что Луна находится в конусообразной тени Земли в два раза дольше, чем необходимо, чтобы поверхность Луны была полностью покрыта тенью. Он сделал вывод: диаметр конусообразной тени Земли в два раза больше диаметра Луны, таким образом, отношение между этими диаметрами (а следовательно, и радиусами) равно 2:1. Сегодня известно, что отношение радиуса Земли к радиусу Луны равно 2,6:1. Во время лунного затмения с помощью хронометра можно определить отношения интервала между первым и последним соприкосновением границы Луны с конусообразной тенью Земли (этот интервал укажет диаметр конусообразной тени Земли) и интервала, в течение которого поверхность Луны окажется полностью покрыта тенью. Проведя расчеты, нетрудно получить значение, близкое к 2,6:1.

Используя обозначения, указанные на иллюстрации, установим следующие соотношения (х — вспомогательная переменная, которая используется для упрощения расчетов):

Подставив в эту систему уравнений соотношения Ts = 400T_L и Rs= 400R_L, исключим вспомогательную переменную х. Упростив выражения, получим:

Эта формула позволяет выразить все приведенные выше расстояния через радиус Земли:

Сюда нужно подставить радиус нашей планеты, чтобы определить все расстояния и радиусы небесных тел в системе «Земля — Луна — Солнце». Аристарху Самосскому не удалось вычислить радиус Земли, следовательно, он получил лишь ряд соотношений, но не расстояния и радиусы в явном виде. Сегодня радиус Земли до экватора известен: он равен 6645 км. Подставив это значение в приведенные выше выражения, получим следующие результаты: R_L = 1850 км (реальное значение 1738 км), расстояние TL = 424000 км (реальное значение — 384000 км), Rs = 740000 км (реальное значение — 696000 км), расстояние TS = 169600000 км (реальное значение — 149680000 км).

Мы привели эти результаты не для того, чтобы сравнить их с фактическими значениями, а для того чтобы показать, насколько умело действовал грек, получивший настолько точные значения примитивными методами.

Источник

Как вращаются Земля, Луна и Солнце

Луна, Земля, Солнце — три важнейших небесных тела, определяющих существование человечества. Первое поддерживает стабильность вращения нашей планеты, влияет на приливы и отливы, второе — наш родной дом, а третье обеспечивает поступление к нам тепла и света.

Размеры Солнца и Луны

Для понимания природы солнечных затмений нужно знать, во сколько раз Луна меньше Солнца. Диаметр центральной звезды нашей системы составляет 1,4 млн км, аналогичный параметр земного спутника — почти 3,5 тыс. км, разница составляет примерно 400 раз.

В то же время Луна находится ближе к Земле, почти в те же 400 раз (при нахождении этих объектов в некоторых точках относительно планеты): на расстоянии около 385 тыс. км, в то время как дистанция от нас до центра Солнечной системы равна 150 млн км.

И хотя светило расположено от нас намного дальше, чем спутник, земному наблюдателю они часто кажутся на небе равными по величине.

Это и есть объяснение солнечных затмений: спутник полностью или частично перекрывает собой Солнце.

Смена лунных фаз

В разных положениях Солнца, Земли и Луны относительно друг друга светлую часть нашего спутника мы видим по-разному.

Части, освещенные светом центральной звезды, называются лунными фазами, это:

• новолуние;
• первая четверть;
• полнолуние;
• последняя четверть.

Иногда выделяют 2 промежуточные фазы: растущую (молодую) и убывающую (стареющую) луну.

Во время новолуния спутник земному наблюдателю не виден, потому что находится между планетой и Солнцем, и к планете обращена его темная сторона, не освещенная звездой. Некоторое свечение лунного диска в этот период все же можно заметить, оно имеет характерный пепельный оттенок, который небесному телу придает солнечный свет, отраженный от Земли.

Через два дня наступает фаза растущей луны, или неомения — это первое после новолуния появление объекта на небе, когда он имеет вид узкого серпа. С каждым днем он увеличивается в размерах и через 7 суток принимает вид полукруга, появляющегося вскоре после заката на западе или юго-западе.

Относительно светила Луна в этой фазе расположена на 90° в восточном направлении, ее видно только вечером и в первой половине ночи.

Через 2 недели после начала лунного цикла наступает полнолуние: Луна расположена в противостоянии с нашей звездой, в сторону Земли обращено все ее освещенное полушарие. Она восходит в момент захода солнца, видна всю ночь и заходит на рассвете.

Еще через неделю начинается фаза последней четверти: спутник имеет вид полукруга, видимого в восточной части неба во второй половине ночи и перед восходом.

Он будет постепенно уменьшаться в размерах и в последние дни примет вид тонкой буквы «С».

Все указанное справедливо для наблюдения из северного полушария Земли. В южном полушарии положения серпа и полукруга противоположные: букву «С» напоминает не убывающий, а растущий месяц.

Совсем иной вид спутник в разных фазах имеет на экваторе, там положение его освещенной части не вертикальное, а горизонтальное. Например, стареющая луна имеет вид узкой лодки, расположенной в нижней половине диска.

Для расчетов принята продолжительность каждой из 4 основных лунных фаз в 7,38 земных дней, но их фактическая длительность постоянно немного меняется из-за вытянутости орбиты спутника и непостоянства его орбитальной скорости.

Так как лунный месяц короче большинства земных (29,5 дней вместо 30 или 31), 1 раз в год в календарном месяце может случиться второе полнолуние. Это явление получило название «Голубая Луна».

Такое наименование обусловлено не изменением оттенка земного спутника, а происхождением из английского фразеологизма «Однажды при голубой луне», смысл которого можно трактовать как «После дождичка в четверг», т. е. никогда. Голубой цвет сателлит может принимать, но это явление крайне редкое и объясняется оптическим эффектом.

Орбитальные характеристики Луны, Земли и Солнца, схема взаимного вращения

Луна совершает 3 вида движений:

• вращается вокруг своей оси, совершая полный оборот примерно за 27,3 земных дней;
• обращается вокруг нашей планеты по эллиптической орбите с точно таким же (27,3 суток) периодом;
• обращается вокруг Солнца в связке «Земля-Луна».

Равенство периодов собственного вращения и обращения Луны вокруг Земли объясняет, почему она всегда повернута к нам одной стороной.

Земля совершает 2 вида движения: вокруг своей оси и вокруг Солнца. В первом случае движение происходит в направлении с запада на восток, и это явление объясняет смену времени суток. На освещенной половине земного шара наблюдается день, а на обратном — ночь.

Каждый такой оборот называется сутками, он длится 23 часа 56 минут и несколько секунд, но для расчетов длительность этого периода принята равной 24 часа.

Вращение планеты вокруг Солнца происходит по эллиптической орбите, среднее расстояние от центральной звезды — около 149,6 млн км, орбитальная скорость — в среднем 29,8 км/с. При этом в перигелии (ближайшей к светилу точке) Земля движется быстрее, со скоростью более 30 км/с, а в самой удаленной позиции (афелии) — медленнее 29,3 км/с.

За время 1 полного витка вокруг Солнца планета делает 365,25 собственных оборотов — это количество дней в 1 астрономическом году. Календарный аналогичный период, в котором сутки приняты равными 24 часам, длится 365 дней, но через каждые 3 годовых срока в календарь добавляется четвертый особый — високосный, с дополнительным 366-м днем.

Солнце неподвижно относительно Земли, но оно также не стоит на месте, а вращается вокруг центра галактики, и 1 такой оборот занимает 220-230 млн лет.

За время своего существования светило успело совершить только 20 полных витков вокруг Млечного Пути.

Ученые отводят нашей звезде срок жизни от сегодняшнего дня 7 млрд лет, за которые она сделает еще примерно 30 таких оборотов.

Линейная скорость движения Солнца в пространстве — 200-220 км/с. Направление его пути называется апекс, оно перемещается в направлении созвездия Геркулес.

Кроме того, светило вращается вокруг собственной оси, ученые определили это по изменению положения пятен на нем. Передвигается оно не как твердая модель: вращение на экваторе быстрее, по направлению к полюсам движение замедляется. Это касается лишь поверхности и массы, близкой к ней.

Внутренние слои и солнечное ядро при вращении ведут себя как классическое твердое тело. Похоже вращаются газовые гиганты Сатурн и Юпитер. Один полный виток вокруг оси Солнце совершает за 25,4 земных дней, его ось не вертикальная, а наклонена на 7°.

Источник

О размерах и расстояниях (Аристарх) — On the Sizes and Distances (Aristarchus)

О размерах и расстояниях (Солнца и Луны) (Περὶ μεγεθῶν καὶ ἀποστημάτων [ἡλίου καὶ σελήνης], Peri megethon kai apostematon ) широко признается как единственная сохранившаяся работа, написанная древним греком-астрономом Аристархом в 310 г. –230 г. до н. Э. В этой работе вычисляются размеры Солнца и Луны , а также их расстояния от Земли в единицах радиуса Земли.

Книга была предположительно сохранена студентами курса математики Паппа Александрийского , хотя свидетельств этого нет. В первое издание было опубликовано Джон Уоллис в 1688, используя несколько средневековых рукописей , собранных сэром Генри Сэвил . Самый ранний латинский перевод был сделан Джорджо Валла в 1488 Существует также 1572 латинский перевод и комментарий по Фредерико Commandino .

СОДЕРЖАНИЕ

Символы

Метод работы основывался на нескольких наблюдениях:

• Видимый размер Солнца и Луны на небе.
• Размер тени Земли относительно Луны во время лунного затмения
• Угол между Солнцем и Луной во время полумесяца очень близок к 90 °.

Остальная часть статьи детализирует реконструкцию метода и результатов Аристарха. Реконструкция использует следующие переменные:

Месяц

Аристарх начал с предположения, что во время полумесяца Луна образует прямоугольный треугольник с Солнцем и Землей. Наблюдая за углом между Солнцем и Луной, φ , отношение расстояний до Солнца и Луны может быть вычислено с помощью одной из форм тригонометрии .

Из диаграммы и тригонометрии мы можем вычислить, что

S L знак равно 1 потому что ⁡ φ знак равно сек ⁡ φ . <\ displaystyle <\ frac > = <\ frac <1><\ cos \ varphi>> = \ sec \ varphi.>

Диаграмма сильно преувеличена, потому что на самом деле S = 390 L , а φ очень близко к 90 °. Аристарх определил φ на тридцатую часть квадранта (в современных терминах, на 3 °) меньше прямого угла: в современной терминологии 87 °. Тригонометрические функции еще не были изобретены, но, используя геометрический анализ в стиле Евклида , Аристарх определил, что

18 S L 20. <\ displaystyle 18

Другими словами, расстояние до Солнца было где-то в 18-20 раз больше, чем расстояние до Луны. Это значение (или значения, близкие к нему) были приняты астрономами в течение следующих двух тысяч лет, пока изобретение телескопа не позволило более точную оценку солнечного параллакса .

Аристарх также рассуждал, что, поскольку угловые размеры Солнца и Луны были одинаковыми, но расстояние до Солнца было в 18-20 раз дальше, чем Луна, Солнце, следовательно, должно быть в 18-20 раз больше.

Лунное затмение

Затем Аристарх использовал другую конструкцию, основанную на лунном затмении:

По подобию треугольников и D L знак равно т т — d <\ displaystyle <\ frac > = <\ frac

> \ quad> D S знак равно т s — т . <\ displaystyle \ quad <\ frac > = <\ frac >.>

Разделив эти два уравнения и используя наблюдение, что видимые размеры Солнца и Луны одинаковы , дает L S знак равно ℓ s <\ displaystyle <\ frac > = <\ frac <\ ell>>>

ℓ s знак равно т — d s — т ⇒ s — т s знак равно т — d ℓ ⇒ 1 — т s знак равно т ℓ — d ℓ ⇒ т ℓ + т s знак равно 1 + d ℓ . <\ displaystyle <\ frac <\ ell>> = <\ frac > \ \ \ Rightarrow \ \ <\ frac > = <\ frac <\ ell>> \ \ \ Rightarrow \ \ 1 — <\ frac > = <\ frac <\ ell>> — <\ frac <\ ell>> \ \ \ Rightarrow \ \ <\ frac <\ ell>> + <\ frac > = 1 + <\ frac <\ ell>>.>.

Крайнее правое уравнение может быть решено относительно ℓ / t

т ℓ ( 1 + ℓ s ) знак равно 1 + d ℓ ⇒ ℓ т знак равно 1 + ℓ s 1 + d ℓ . <\ displaystyle <\ frac <\ ell>> (1 + <\ frac <\ ell>>) = 1 + <\ frac <\ ell>> \ \ \ Rightarrow \ \ < \ frac <\ ell>> = <\ frac <1 + <\ frac <\ ell>>> <1 + <\ frac <\ ell>>>>.>.

т s ( 1 + s ℓ ) знак равно 1 + d ℓ ⇒ s т знак равно 1 + s ℓ 1 + d ℓ . <\ displaystyle <\ frac > (1 + <\ frac <\ ell>>) = 1 + <\ frac <\ ell>> \ \ \ Rightarrow \ \ <\ frac > = <\ frac <1 + <\ frac <\ ell>>> <1 + <\ frac <\ ell>>>>.>.>

Внешний вид этих уравнений можно упростить, используя n = d / ℓ и x = s / ℓ .

ℓ т знак равно 1 + Икс Икс ( 1 + п ) <\ displaystyle <\ frac <\ ell>> = <\ frac <1 + x>>> s т знак равно 1 + Икс 1 + п <\ displaystyle <\ frac > = <\ frac <1 + x><1 + n>>>

Приведенные выше уравнения полностью определяют радиусы Луны и Солнца в виде наблюдаемых величин.

Читайте также:  Блэк десерт торговец убывающей луны

Следующие формулы дают расстояния до Солнца и Луны в земных единицах:

L т знак равно ( ℓ т ) ( 180 π θ ) <\ displaystyle <\ frac > = \ left ( <\ frac <\ ell>> \ right) \ left ( <\ frac <180><\ pi \ theta>> \ right) > S т знак равно ( s т ) ( 180 π θ ) <\ displaystyle <\ frac > = \ left ( <\ frac > \ right) \ left ( <\ frac <180><\ pi \ theta>> \ right)>

где θ — видимый радиус Луны и Солнца, измеренный в градусах.

Маловероятно, что Аристарх использовал эти точные формулы, но эти формулы, вероятно, являются хорошим приближением к формулам Аристарха.

Полученные результаты

Приведенные выше формулы могут быть использованы для реконструкции результатов Аристарха. В следующей таблице показаны результаты давней (но сомнительной) реконструкции с использованием n = 2, x = 19,1 ( φ = 87 °) и θ = 1 °, наряду с современными принятыми значениями.

Количество	Связь	Реконструкция	Современное
с / т	Радиус Солнца в радиусах Земли	6,7	109
т / ℓ	Радиус Земли в радиусах Луны	2,85	3,50
Л / т	Расстояние Земля-Луна в радиусах Земли	20	60,32
S / т	Расстояние Земля-Солнце в радиусах Земли	380	23 500

Ошибка в этом вычислении происходит в первую очередь из-за плохих значений x и θ . Плохое значение θ особенно удивительно, поскольку Архимед пишет, что Аристарх был первым, кто определил, что Солнце и Луна имеют видимый диаметр в полградуса. Это даст значение θ = 0,25 и соответствующее расстояние до Луны в 80 радиусов Земли, что намного лучше. Несогласие в работе с Архимедом, по-видимому, связано с утверждением Аристарха о том, что лунно-солнечный диаметр составляет 1/15 «мероса» зодиака, что означает 1/15 зодиакального знака (30 °), не зная, что Греческое слово «мерос» означало либо «часть», либо 7 ° 1/2; и 1/15 последней суммы составляет 1 ° / 2, что согласуется с показаниями Архимеда.

Аналогичная процедура была позже использована Гиппархом , который по оценкам среднего расстояния до Луны , как 67 радиусов Земли, и Птолемея , который принял 59 радиусов Земли для этого значения.

Иллюстрации

Некоторые интерактивные иллюстрации предложений в разделе « Размеры» можно найти здесь:

• Гипотеза 4 утверждает, что когда Луна кажется нам уменьшенной вдвое, ее расстояние от Солнца будет меньше квадранта на одну тридцатую квадранта [то есть меньше 90 ° на 1/30 от 90 ° или на 3 °. , и поэтому равен 87 °] (Heath 1913: 353).
• Предложение 1 утверждает, что две равные сферы охватываются одним и тем же цилиндром, а две неравные сферы — одним и тем же конусом, вершина которого находится в направлении меньшей сферы; и прямая линия, проведенная через центры сфер, проходит под прямым углом к ​​каждой из окружностей, в которых поверхность цилиндра или конуса касается сфер (Heath 1913: 354).
• Утверждение 2 гласит, что если сфера освещена сферой, большей, чем она сама, то освещенная часть первой сферы будет больше, чем полусфера (Heath 1913: 358).
• Утверждение 3 гласит, что круг на Луне, разделяющий темную и яркую части, является наименьшим, когда конус, охватывающий и Солнце, и Луну, имеет вершину у нашего глаза (Heath 1913: 362).
• Утверждение 4 гласит, что круг, разделяющий темную и яркую части на Луне, заметно не отличается от большого круга на Луне (Heath 1913: 365).
• Утверждение 6 гласит, что Луна движется [по орбите] ниже, чем [орбита] Солнца, и, когда она уменьшена вдвое, находится на расстоянии меньше квадранта от Солнца (Heath 1913: 372).
• Предложение 7 гласит, что расстояние от Солнца до Земли больше, чем в 18 раз, но меньше, чем в 20 раз, расстояния Луны от Земли (Heath 1913: 377). Другими словами, Солнце находится в 18-20 раз дальше и шире Луны.
• Утверждение 13 гласит, что прямая линия, соединяющая часть, пересеченную в пределах земной тени, окружности круга, в котором края круга, разделяющего темную и яркую части Луны, движутся меньше чем вдвое диаметра окружности. Луна, но имеет отношение к ней большее, чем отношение 88 к 45; и он составляет менее 1/9 части диаметра Солнца, но имеет отношение к нему больше, чем 21, к 225. Но у него есть прямая линия, проведенная из центра Солнца под прямым углом к ось и встречающиеся со сторонами конуса отношение больше, чем отношение 979 к 10 125 (Heath 1913: 394).
• Предложение 14 гласит, что прямая линия, соединяющая центр Земли с центром Луны, имеет прямую, отрезанную от оси к центру Луны прямой линией, проходящей через [окружность] в тени Земли a отношение больше, чем у 675 к 1 (Heath 1913: 400).
• Предложение 15 утверждает, что диаметр Солнца имеет отношение к диаметру Земли больше 19/3, но меньше 43/6 (Heath 1913: 403). Это означает, что Солнце (в среднем) в 6¾ раз шире Земли или что Солнце имеет ширину 13½ земного радиуса. Тогда Луна и Солнце должны быть на расстоянии 20¼ и 387 земных радиусов от нас, чтобы иметь угловой размер в 2º.
• Предложение 17a в средневековой арабской версии книги Ат -Туси о размерах утверждает, что отношение расстояния вершины теневого конуса от центра Луны (когда Луна находится на оси [то есть в середине затмение] конуса, содержащего Землю и Солнце) к расстоянию от центра Луны до центра Земли больше отношения 71 к 37 и меньше отношения 3 к одному (Berggren & Sidoli 2007: 218). Другими словами, кончик теневого конуса Земли находится между 108/37 и в четыре раза дальше, чем Луна.

Источник