Почему планеты вращаются вокруг Солнца?
Сегодня нет ни малейших сомнений в том, что Земля вращается вокруг Солнца. Если еще не так давно, в масштабах истории Вселенной, люди были уверены, что центром нашей Галактики является Земля, то сегодня нет никаких сомнений, что все происходит с точностью до наоборот.
От Птолемея до Ньютона
Представления о том, как расположены планеты на небосводе первым в своем трактате «Великое математическое построение по астрономии», высказал древнегреческий астроном Птолемей. Он первым предположил, что они совершают свои движения по кругу. Но Птолемей ошибочно считал, что все планеты, а также Луна и Солнце движутся вокруг Земли. Долгое время его трактат считался общепринятым как в арабском, так и западном мире.
Точку в этом спорном для человечества факте поставил Николай Коперник. Польский астроном создал свою гелиоцентрическую систему, в которой убедительно доказал, что Земля не является центром Вселенной, а все планеты, по его твердому убеждению, вращаются по орбитам вокруг Солнца. Работа польского ученого «О вращении небесных сфер», была издана в немецком Нюрнберге в 1543 году.
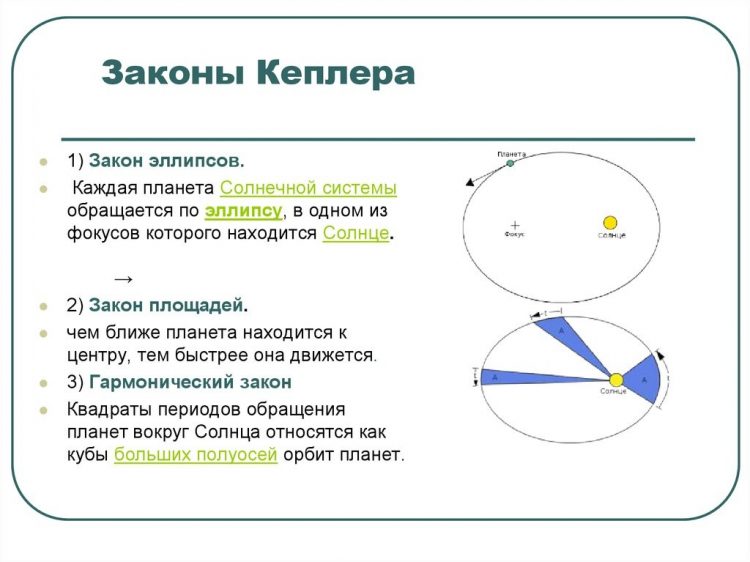
После смерти Коперника его труды продолжил датчанин Тихо Браге. Астроном, являющийся весьма состоятельным человеком, оборудовал принадлежащий ему остров, внушительными бронзовыми кругами, на которые наносил результаты наблюдения за небесными телами. Результаты, полученные Браге, помогли в исследовании математику Иоганну Кеплеру,который вывел три своих знаменитых закона движения планет.
Англичанин Исаак Ньютон, открыв закон всемирного тяготения, существенно продвинул представления человечества об эллиптических орбитах небесных тел. Его объяснения, что приливы и отливы на Земле происходят под влиянием Луны, оказались убедительными для научного мира.
Почему планеты вращаются вокруг Солнца
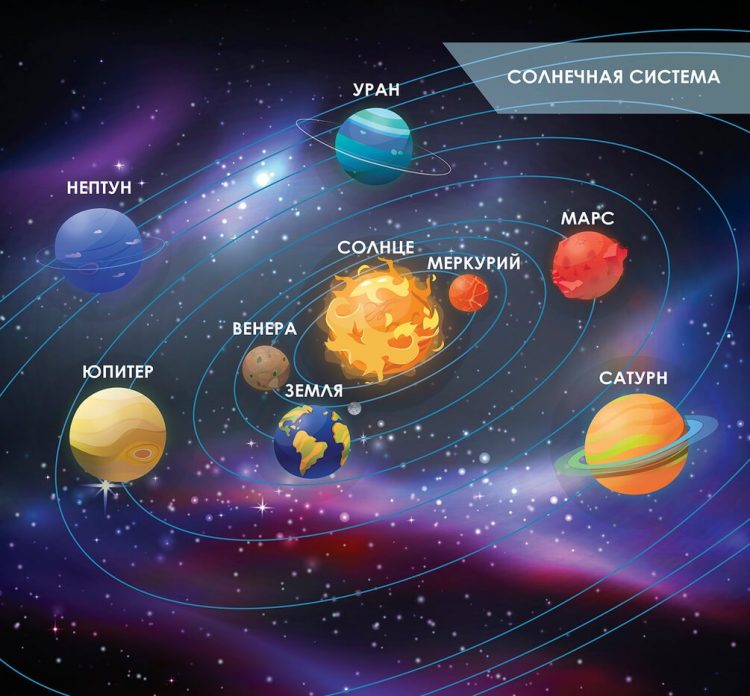
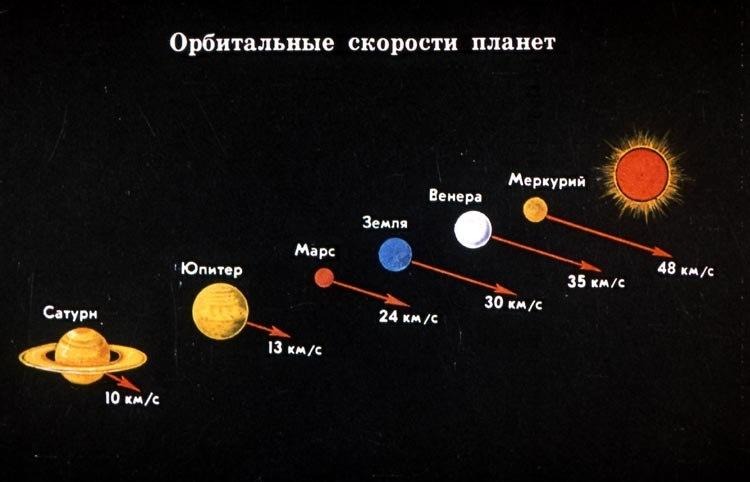
Как Земля, так и все остальные планеты нашей солнечной системы движутся по своей траектории вокруг Солнца. Скорость их движения и траектория могут быть разными, однако все они держатся у нашего естественного светила.
Движение планет по орбите вокруг Солнца происходит под воздействием двоих сил:
- до центровой (сила тяготения Солнца);
- от центровой (силы инерции во время поступательного движения).
Срок, за который планеты совершают полный оборот вокруг Солнца, естественно различный. У Меркурия, самой ближней к звезде, он составляет 88 земных суток. Наша Земля проходит цикл за 365 дней и 6 часов. Самая крупная в Солнечной системе планета Юпитер завершает свой оборот за 11,9 земных лет. Ну а у Плутона, — наиболее удаленной от Солнца планеты оборот и вовсе составляет 247,7 года. +
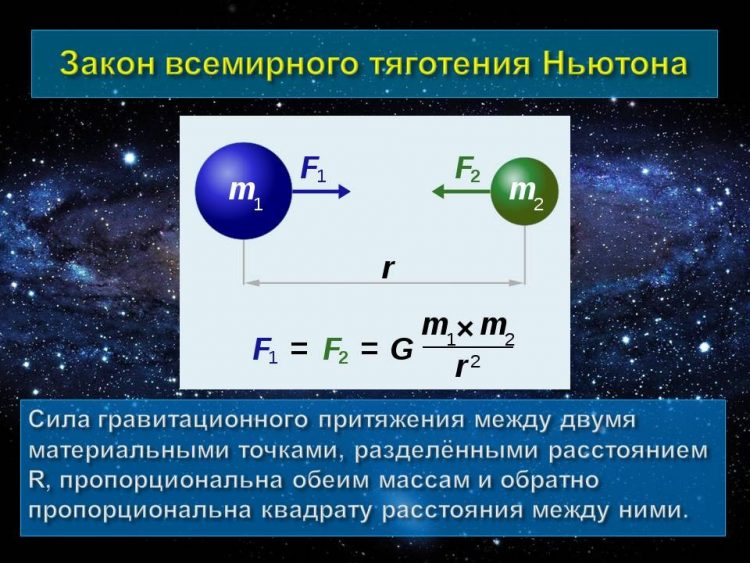
Закон всемирного тяготения
Солнце является самым крупным объектом в нашей галактике. Масса нашего светила в разы превышает массу всех остальных тел в совокупности. А в физике, как известно, действует сила всемирного тяготения, которую никто не отменял, в том числе, и для Космоса.
Ее закон гласит, что тела с меньшей массой притягиваются к телам с большей массой. Именно поэтому все планеты, спутники и другие космические объекты и притягиваются к Солнцу, самому крупному из них.
Сила тяготения, к слову, аналогичным образом работает и на Земле.
Вспомните, что происходит с теннисным мячиком, брошенным в воздух. Он падает, притягиваясь к поверхности нашей планеты.
Понимая принцип стремления планет к Солнцу, возникает очевидный вопрос: почему они не падают на поверхность звезды, а движутся вокруг нее по собственной траектории. И этому также имеется вполне доступное объяснение.
Инерция
Согласно теории об образовании нашей звезды, около 4,57 млрд. лет назад в космосе возникло огромное количество пыли, которое постепенно превратилось в диск, а затем – в Солнце. Внешние частички этой пыли стали соединяться между собой, образуя планеты. Уже тогда они по инерции начали вращаться вокруг звезды и продолжают двигаться по той же траектории и сегодня.
Следует также учесть, что все планеты в нашей Солнечной системе движутся, не вокруг светила, а вокруг так называемого центра масс. Каждая при этом, вращаясь вокруг своей оси, слегка раскачиваются (подобно юле). К тому же и сама ось может ненамного смещаться.
Что же касается орбиты каждого из объектов, то траектория их движения зависит от скорости и массы. А эти показатели у всех объектов, как вы понимаете, разные. Вот почему Земля и другие планеты движутся вокруг Солнца, и никак иначе.
Таким образом, инерционное движение отдалят планету от Солнца, но до центровая сила искривляет траекторию и удерживает планету на орбите. Все планеты вращаются вокруг Солнца в одном направлении, по тому же направлению и обращаются планеты вокруг своей оси (исключение Венера и Уран).
Практически каждая планета в период своего формирования подвергалась множеству ударов астероидов, в результате которых изменялась ее форма и радиус орбиты. Немаловажную роль играет также и тот факт близкого формирования группы планет и большого скопления космического мусора, в результате чего расстояние между ними минимальное, что, в свою очередь, приводит к нарушению гравитационного поля.
Движение планеты Земля вокруг Солнца и его значение
Земля как планета Солнечной системы по расчетам ученых сформировалась более 4,5 млрд лет назад. За это время расстояние от светила практически не изменялось. Скорость движения планеты и сила притяжения Солнца уравновесили ее орбиту. Она не идеально круглая, но стабильная.
Если бы сила притяжения светила была сильнее или скорость Земли заметно уменьшилась, то она бы упала на Солнце. В противном случае она рано или поздно улетела бы в космос, перестав быть частью системы.
Расстояние от Солнца до Земли делает возможным поддержание оптимальной температуры на ее поверхности.
Путь планеты вокруг светила называется орбитой. Траектория этого полета не идеально круглая. Она имеет эллипсность. Максимальная разница составляет 5 млн км.
Самая близкая точка орбиты к Солнцу находится на расстоянии 147 км. Она называется перигелием. Земля ее проходит в январе. В июле планета находится от светила на максимальном отдалении. Наибольшее расстояние — 152 млн км. Эта точка называется афелием.
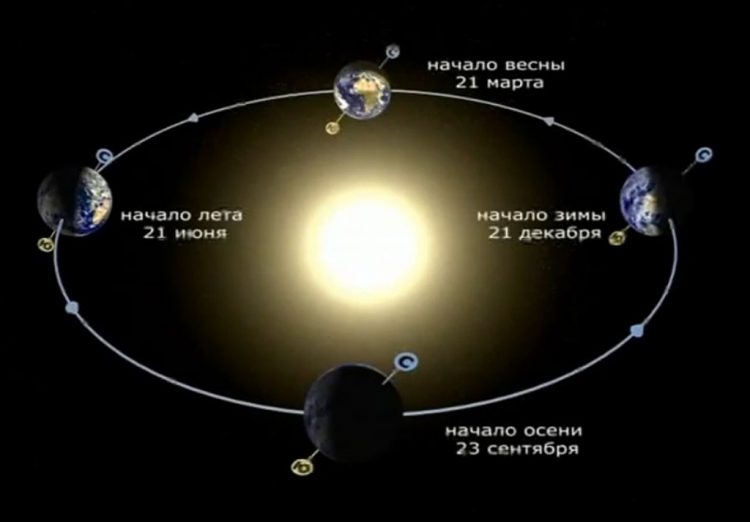
Вращение Земли вокруг своей оси и Солнца обеспечивает соответственно смену суточных режимов и годовых периодов.
Вращение Земли вокруг Солнца
Для человека движение планеты вокруг центра системы незаметно. Это из-за того, что масса Земли огромна. Тем не менее каждую секунду мы пролетаем в пространстве около 30 км. Это кажется нереальным, но таковы расчеты. В среднем считается, что Земля находится от Солнца на расстоянии около 150 млн км. Один полный оборот вокруг светила она делает за 365 дней.
Точное расстояние, которое наша планета проходит за год, двигаясь вокруг светила, составляет 942 млн км. Мы вместе с ней движемся в пространстве по эллиптической орбите со скоростью 107 000 км/час. Направление вращения — с запада на восток, то есть против условной часовой стрелки.
Таким образом, наша планета находится в постоянном движении. Вместе с Солнцем она перемещается в космосе вокруг центра Галактики. А та, в свою очередь, движется во Вселенной. Но наибольшее значение для всего живого играет вращение Земли вокруг Солнца и собственной оси. Без этого движения условия на планете были бы непригодными для поддержания жизни.
Видео
Источник
Земля вращается вокруг солнца закон всемирного тяготения
§ 14. Д вижение небесных тел под действием сил тяготения
1. Закон всемирного тяготения
С огласно закону всемирного тяготения, изученному в курсе физики,
все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:
F = G 
,
где m 1 и m 2 — массы тел; r — расстояние между ними; G — гравитационная постоянная.
Открытию закона всемирного тяготения во многом способствовали законы движения планет, сформулированные Кеплером, и другие достижения астрономии XVII в. Так, знание расстояния до Луны позволило Исааку Ньютону (1643—1727) доказать тождественность силы, удерживающей Луну при её движении вокруг Земли, и силы, вызывающей падение тел на Землю.
Ведь если сила тяжести меняется обратно пропорционально квадрату расстояния, как это следует из закона всемирного тяготения, то Луна, находящаяся от Земли на расстоянии примерно 60 её радиусов, должна испытывать ускорение в 3600 раз меньшее, чем ускорение силы тяжести на поверхности Земли, равное 9,8 м/с 2 . Следовательно, ускорение Луны должно составлять 0,0027 м/с 2 .
В то же время Луна, как любое тело, равномерно движущееся по окружности, имеет ускорение
где ω — угловая скорость Луны; r — радиус её орбиты. Если считать, что радиус Земли равен 6400 км, то радиус лунной орбиты будет составлять r = 60 • 6 400 000 м = 3,84 • 10 8 м. Звёздный период обращения Луны T = 27,32 суток, в секундах составляет 2,36 • 10 6 с. Тогда ускорение орбитального движения Луны
a = 
• r = 
• 3,84 • 10 8 м = 0,0027 м/с 2 .
Равенство этих двух величин ускорения доказывает, что сила, удерживающая Луну на орбите, есть сила земного притяжения, ослабленная в 3600 раз по сравнению с действующей на поверхности Земли.
Можно убедиться и в том, что при движении планет, в соответствии с третьим законом Кеплера, их ускорение и действующая на них сила притяжения Солнца обратно пропорциональны квадрату расстояния, как это следует из закона всемирного тяготения. Действительно, согласно третьему закону Кеплера отношение кубов больших полуосей орбит d и квадратов периодов обращения T есть величина постоянная:
= 
= 
= . = const.
Ускорение планеты равно
a = 
= 
= 4 π 2 
.
Из третьего закона Кеплера следует
= 
,
поэтому ускорение планеты равно
a = 4 π 2 • const 
.
Итак, сила взаимодействия планет и Солнца удовлетворяет закону всемирного тяготения.
2. Возмущения в движении тел Солнечной системы
З аконы Кеплера строго выполняются, если рассматривается движение двух изолированных тел (Солнце и планета) под действием их взаимного притяжения. Однако в Солнечной системе планет много, все они взаимодействуют не только с Солнцем, но и между собой. Поэтому движение планет и других тел не в точности подчиняется законам Кеплера. Отклонения тел от движения по эллипсам называются возмущениями .
Возмущения эти невелики, так как масса Солнца гораздо больше массы не только отдельной планеты, но и всех планет в целом. Наибольшие возмущения в движении тел Солнечной системы вызывает Юпитер, масса которого в 300 раз превышает массу Земли. Особенно заметны отклонения астероидов и комет при их прохождении вблизи Юпитера.
В настоящее время возмущения учитываются при вычислении положения планет, их спутников и других тел Солнечной системы, а также траекторий космических аппаратов, запускаемых для их исследования. Но ещё в XIX в. расчёт возмущений позволил сделать одно из самых известных в науке открытий «на кончике пера» — открытие планеты Нептун.
Проводя очередной обзор неба в поиске неизвестных объектов, Вильям Гершель в 1781 г. открыл планету, названную впоследствии Ураном. Спустя примерно полвека стало очевидно, что наблюдаемое движение Урана не согласуется с расчётным даже при учёте возмущений со стороны всех известных планет. На основе предположения о наличии ещё одной «заурановой» планеты были сделаны вычисления её орбиты и положения на небе. Независимо друг от друга эту задачу решили Джон Адамс в Англии и Урбен Леверье во Франции. На основе расчётов Леверье немецкий астроном Иоганн Галле 23 сентября 1846 г. обнаружил в созвездии Водолея неизвестную ранее планету — Нептун. Это открытие стало триумфом гелиоцентрической системы, важнейшим подтверждением справедливости закона всемирного тяготения. В дальнейшем в движении Урана и Нептуна были замечены возмущения, которые стали основанием для предположения о существовании в Солнечной системе ещё одной планеты. В 1930 г. после просмотра большого количества фотографий звёздного неба был обнаружен Плутон, который, как оказалось, является одним из множества объектов, расположенных за орбитой Нептуна.
3. Масса и плотность Земли
З акон всемирного тяготения позволил определить массу нашей планеты. Исходя из закона всемирного тяготения, ускорение свободного падения можно выразить так:
g = G 
.
Подставим в формулу известные значения этих величин: g = 9,8 м/с 2 , G = 6,67 • 10 –11 Н • м 2 /кг 2 , R = 6370 км — и получим, что масса Земли M = 6 • 10 24 кг.
Зная массу и объём земного шара, можно вычислить его среднюю плотность: 5,5 • 10 3 кг/м 3 . С глубиной за счёт увеличения давления и содержания тяжелых элементов плотность возрастает.
4. Определение массы небесных тел
Б олее точная формула третьего закона Кеплера, которая была получена Ньютоном, даёт возможность определить одну из важнейших характеристик любого небесного тела — массу. Выведем эту формулу, считая (в первом приближении) орбиты планет круговыми.
Пусть два тела, имеющие массы m 1 и m 2 , взаимно притягивающиеся и обращающиеся вокруг общего центра масс, находятся от центра масс на расстоянии r 1 и r 2 и обращаются вокруг него с периодом T . Расстояние между их центрами R = r 1 + r 2 . На основании закона всемирного тяготения ускорение каждого из этих тел равно:
a 1 = G 
, a 2 = G 
.
Угловая скорость обращения вокруг центра масс составляет ω = 
. Тогда центростремительное ускорение выразится для каждого тела так:
a 1 = 
r 1 , a 2 = 
r 2 .
Приравняв полученные для ускорений выражения, выразив из них r 1 и r 2 и сложив их почленно, получаем:
G = 
= 
( r 1 + r 2 ),
= 
.
Поскольку в правой части этого выражения находятся только постоянные величины, оно справедливо для любой системы двух тел, взаимодействующих по закону тяготения и обращающихся вокруг общего центра масс, — Солнце и планета, планета и спутник. Определим массу Солнца, для этого запишем выражение:
= 
,
где M — масса Солнца; m 1 — масса Земли; m 2 — масса Луны; T 1 и a 1 — период обращения Земли вокруг Солнца (год) и большая полуось её орбиты; T 2 и a 2 — период обращения Луны вокруг Земли и большая полуось лунной орбиты.
Пренебрегая массой Земли, которая ничтожно мала по сравнению с массой Солнца, и массой Луны, которая в 81 раз меньше массы Земли, получим:
= 
.
Подставив в формулу соответствующие значения и приняв массу Земли за единицу, мы получим, что Солнце примерно в 333 тыс. раз по массе больше нашей планеты.
Массы планет, не имеющих спутников, определяют по тем возмущениям, которые они оказывают на движение астероидов, комет или космических аппаратов, пролетающих в их окрестностях. Об определении массы звёзд см. в § 23.
П од действием взаимного притяжения частиц тело стремится принять форму шара. Если эти тела вращаются, то они деформируются, сжимаются у полюсов.
Кроме того, изменение их формы происходит и под действием взаимного притяжения, которое вызывают явления, называемые приливами . Давно известные на Земле, они получили объяснение только на основе закона всемирного тяготения.
Рис. 3.13. Схема лунных приливов
Рассмотрим ускорения, создаваемые притяжением Луны в различных точках земного шара (рис. 3.13). Поскольку точки A , B и O находятся на различных расстояниях от Луны, ускорения, создаваемые её притяжением, будут различны.
Разность ускорений, вызываемых притяжением другого тела в данной точке и в центре планеты, называется приливным ускорением.
Приливные ускорения в точках A и B направлены от центра Земли. В результате Земля, и в первую очередь её водная оболочка, вытягивается в обе стороны по линии, соединяющей центры Земли и Луны. В точках A и B наблюдается прилив, а вдоль круга, плоскость которого перпендикулярна этой линии, на Земле происходит отлив. Тяготение Солнца также вызывает приливы, но из-за большей его удалённости они меньше, чем вызванные Луной. Приливы наблюдаются не только в гидросфере, но и в атмосфере и в литосфере Земли и других планет.
Вследствие суточного вращения Земля стремится увлечь за собой приливные горбы, в то же время вследствие тяготения Луны, которая обращается вокруг Земли за месяц, полоса приливов должна перемещаться по земной поверхности значительно медленнее. В результате между огромными массами воды, участвующей в приливных явлениях, и дном океана возникает приливное трение. Оно тормозит вращение Земли и вызывает увеличение продолжительности суток, которые в прошлом были значительно короче (5—6 ч). Тот же эффект ускоряет орбитальное движение Луны и приводит к её медленному удалению от Земли. При этом приливы со стороны Земли на Луне затормозили её вращение, и она теперь обращена к Земле одной стороной. Такое же медленное вращение характерно для многих спутников Юпитера и других планет. Сильные приливы, вызываемые на Меркурии и Венере Солнцем, по-видимому, являются причиной их крайне медленного вращения вокруг оси.
6. Движение искусственных спутников Земли и космических аппаратов к планетам
В озможность создания искусственного спутника Земли теоретически обосновал ещё Ньютон. Он показал, что существует такая горизонтально направленная скорость 
, при которой тело, падая на Землю, тем не менее на неё не упадёт, а будет двигаться вокруг Земли, оставаясь от неё на одном и том же расстоянии. При такой скорости тело будет приближаться к Земле вследствие её притяжения как раз на столько, на сколько из-за кривизны поверхности нашей планеты оно будет от неё удаляться (рис. 3.14). Эта скорость, которую называют первой космической (или круговой), известна вам из курса физики:
v 1 = 
= 7,9 • 10 3 м/с = 7,9 км/с.
Рис. 3.14. Орбита искусственного спутника Земли
Практически осуществить запуск искусственного спутника Земли оказалось возможно лишь через два с половиной столетия после открытия Ньютона — 4 октября 1957 г. За время, прошедшее с этого дня, который нередко называют началом космической эры человечества, искусственные спутники самого различного устройства и назначения заняли важное место в нашей повседневной жизни. Они обеспечивают непрерывный мониторинг погоды и других природных явлений, трансляции телевидения и т. п. Спутниковая навигационная система ГЛОНАСС и другие системы глобального позиционирования позволяют в любой момент с высокой степенью точности определить координаты любой точки на Земле. Пожалуй, нет в наши дни ни одной глобальной проблемы, в решении которой не принимали участие искусственные спутники Земли (ИСЗ).
Космические аппараты (КА), которые направляются к Луне и планетам, испытывают притяжение со стороны Солнца и согласно законам Кеплера так же, как и сами планеты, движутся по эллипсам. Скорость движения Земли по орбите составляет около 30 км/с. Если геометрическая сумма скорости космического аппарата, которую ему сообщили при запуске, и скорости Земли будет больше этой величины, то КА будет двигаться по орбите, лежащей за пределами земной орбиты. Если меньше — то внутри орбиты Земли. В первом случае, если аппарат летит к Марсу (рис. 3.15) или другой внешней планете, энергетические затраты будут наименьшими, если КА достигнет орбиты этой планеты при своём максимальном удалении от Солнца — в афелии. Кроме того, необходимо так рассчитать время старта КА, чтобы к этому моменту в ту же точку своей орбиты пришла планета. Иначе говоря, начальная скорость и день запуска КА должны быть выбраны таким образом, чтобы КА и планета, двигаясь каждый по своей орбите, одновременно подошли к точке встречи. Во втором случае — для внутренней планеты — встреча с КА должна произойти в перигелии его орбиты (рис. 3.16). Такие траектории полётов называются полуэллиптическими . Большие оси этих эллипсов проходят через Солнце, которое находится в одном из фокусов, как и полагается по первому закону Кеплера.
Рис. 3.15. Траектория полёта KA к Марсу
Рис. 3.16. Траектория полёта KA к Венере
Конструкция и оборудование современных КА обеспечивают возможность совершения ими весьма сложных манёвров — выход на орбиту спутника планеты, посадка на планету, передвижение по её поверхности и т. п.
В опросы 1. Почему движение планет происходит не в точности по законам Кеплера? 2. Как было установлено местоположение планеты Нептун? 3. Какая из планет вызывает наибольшие возмущения в движении других тел Солнечной системы и почему? 4. Какие тела Солнечной системы испытывают наибольшие возмущения и почему? 5. По каким траекториям движутся космические аппараты к Луне; к планетам? 6*. Объясните причину и периодичность приливов и отливов. 7*. Будут ли одинаковы периоды обращения искусственных спутников Земли и Луны, если эти спутники находятся на одинаковых расстояниях от них?
У пражнение 12 1. Определите массу Юпитера, зная, что его спутник, который отстоит от Юпитера на 422 000 км, имеет период обращения 1,77 суток. Для сравнения используйте данные для системы Земля—Луна. 2. Ускорение силы тяжести на Марсе составляет 3,7 м/с 2 , на Юпитере — 25 м/с 2 . Рассчитайте первую космическую скорость для этих планет. 3. Сколько суток (примерно) продолжается полёт КА до Марса, если он проходит по эллипсу, большая полуось которого равна 1,25 а. е.?
Источник