Высота солнца над горизонтом: изменение и измерение. Восход солнца в декабре
Жизнь на нашей планете зависит от количества солнечного света и тепла. Страшно представить даже на миг, что было бы, если бы на небе не было такой звезды, как Солнце. Каждая травинка, каждый листочек, каждый цветочек нуждается в тепле и свете, как люди в воздухе.
Угол падения лучей солнца равен высоте солнца над горизонтом
Количество солнечного света и тепла, которое поступает на земную поверхность, прямо пропорционально углу падения лучей. Солнечные лучи могут падать на Землю под углом от 0 до 90 градусов. Угол попадания лучей на землю разный, потому что наша планета имеет форму шара. Чем он больше, тем светлее и теплее.
Таким образом, если луч идёт под углом 0 градусов, он только скользит вдоль поверхности земли, не нагревая её. Такой угол падения бывает на Северном и Южном полюсах, за полярным кругом. Под прямым углом солнечные лучи падают на экватор и на поверхность между Южным и Северным Тропиком.
Если угол попадания солнечных лучей на землю прямой, это говорит о том, что солнце в зените.
Таким образом, угол падения лучей на поверхность земли и высота солнца над горизонтом равны между собой. Зависят они от географической широты. Чем ближе к нулевой широте, тем угол падения лучей ближе к 90 градусам, тем выше находится солнце над горизонтом, тем теплее и светлее.
Как солнце изменяет свою высоту над горизонтом
Высота солнца над горизонтом не является постоянной величиной. Напротив, она всегда изменяется. Причина этого кроется в непрерывном движении планеты Земля вокруг звезды Солнце, а также вращении планеты Земля вокруг собственной оси. В результате день сменяет ночь, а времена года друг друга.
Территория между тропиками получает больше всех тепла и света, здесь день и ночь практически равны друг другу по продолжительности, а солнце находится в зените 2 раза в год.
Поверхность за полярным кругом получает всех меньше тепла и света, здесь существуют такие понятия, как полярные день и ночь, которые длятся около полугода.
Дни осеннего и весеннего равноденствия
Выделены 4 основные астрологические даты, которые определяет высота солнца над горизонтом. 23 сентября и 21 марта – дни осеннего и весеннего равноденствия. Это означает, что высота солнца над горизонтом в сентябре и марте в эти дни 90 градусов.
Южное и Северное полушария освещаются солнцем одинаково, а долгота ночи равна долготе дня. Когда в Северном полушарии наступает астрологическая осень, то в Южном, наоборот, весна. То же самое можно сказать о зиме и лете. Если в Южном полушарии зима, то в Северном – лето.
Дни летнего и зимнего солнцестояния
22 июня и 22 декабря – дни летнего и зимнего солнцестояния. 22 декабря наблюдается самый короткий день и самая длинная ночь в Северном полушарии, а зимнее солнце находится на самой низкой высоте над горизонтом за весь год.
Выше широты 66,5 градуса солнце находится под горизонтом и не восходит. Это явление, когда зимнее солнце не восходит на горизонт, называется полярной ночью. Самая короткая ночь бывает на широте 67 градусов и длится всего 2 суток, а самая длинная бывает на полюсах и длится 6 месяцев!
Декабрь является из всего года тем месяцем, когда в Северном полушарии самые длинные ночи. Люди в Центральной России просыпаются на работу в темноте и возвращаются тоже в темное время суток. Это тяжелый месяц для многих, так как нехватка солнечного света сказывается на физическом и моральном состоянии людей. По этой причине может даже развиться депрессия.
В Москве в 2016 г. восход солнца в декабре 1 числа будет в 08.33. При этом долгота дня составит 7 часов 29 минут. Заход солнца за горизонт будет очень рано, в 16.03. Ночь составит 16 часов 31 минуту. Таким образом, получается, что долгота ночи в 2 раза больше, чем долгота дня!
В этом году день зимнего солнцестояния – 21 декабря. Самый короткий день будет длиться ровно 7 часов. Затем 2 дня продержится такая же ситуация. И уже с 24 декабря день пойдёт на прибыль медленно, но верно.
В среднем в сутки будет прибавляться по одной минуте светлого времени. В конце месяца восход солнца в декабре будет ровно в 9 часов, что на 27 минут позже, чем 1-го декабря
22 июня – день летнего солнцестояния. Всё происходит с точностью до наоборот. За весь год именно в эту дату самый длинный день по продолжительности и самая короткая ночь. Это касаемо Северного полушария.
В Южном всё наоборот. С этим днём связаны интересные природные явления. За Полярным кругом наступает полярный день, солнце не заходит за горизонт на Северном полюсе 6 месяцев. В Санкт-Петербурге в июне начинаются загадочные белые ночи. Длятся они примерно с середины июня в течение двух-трёх недель.
Все эти 4 астрологические даты могут меняться на 1-2 дня, так как солнечный год не всегда совпадает с календарным годом. Также смещения происходят в високосные года.
Высота солнца над горизонтом и климатические условия
Солнце является одним из самых важных климатообразующих факторов. В зависимости от того, как изменялась высота солнца над горизонтом над конкретным участком земной поверхности, меняются климатические условия и времена года.
Например, на Крайнем Севере лучи солнца падают под очень маленьким углом и только лишь скользят вдоль поверхности земли, совсем не нагревая её. Под условием этого фактора климат здесь крайне суровый, присутствует вечная мерзлота, холодные зимы с леденящими ветрами и снегами.
Чем больше высота солнца над горизонтом, тем теплее климат. Например, на экваторе он необычайно жаркий, тропический. Сезонные колебания также в районе экватора практически не чувствуются, в этих районах вечное лето.
Измерение высоты солнца над горизонтом
Как говорится, всё гениальное – просто. Так и здесь. Прибор для измерения высоты солнца над горизонтом элементарно прост. Он представляет собой горизонтальную поверхность с шестом посередине длиной 1 метр. В солнечный день в полдень шест отбрасывает самую короткую тень. С помощью этой кратчайшей тени и проводятся расчёт и измерения. Нужно замерить угол между концом тени и отрезком, соединяющим конец шеста с концом тени. Эта величина угла и будет являться углом нахождения солнца над горизонтом. Этот прибор называется гномоном.
Гномон – это древний астрологический инструмент. Существуют и другие приборы для измерения высоты солнца над горизонтом, такие как секстант, квадрант, астролябия.
Источник
Значит чем выше солнце над горизонтом тем
Роза Мария Рос. «Мир математики» № 30
«Музыка сфер. Астрономия и математика»
Систематизация и структурирование результатов астрономических наблюдений возможны только благодаря математике. Более того, математика сыграла важнейшую роль в развитии астрономии. Однако астрономия имеет свои особенности: вы не можете повторить эксперимент в лаборатории в любое удобное время, изменив то или иное условие. А ведь как прекрасно было бы заказывать затмения по желанию!
Хочу частичное солнечное затмение! Нет, лучше полное!
Астрономия родилась одновременно с человечеством. Телевизора у древнего человека не было, и он наверняка проводил вечера, глядя на звёздное небо. По крайней мере, на небо он смотрел чаще, чем любой из нас. Постепенно наши предки начали понимать, что некоторые астрономические явления повторяются и, наблюдая за ними, можно определить, когда начинать сеять, а когда — отправляться на охоту.
Несомненно, все эти знания помогали людям выживать. Так наука впервые доказала свою полезность. Кроме того, древние люди считали, что те явления, которые они не могут объяснить, происходят по воле Бога. Такие события были сакральными, их связывали с выполнением определённых ритуалов, которые и стали задачей жрецов различных примитивных культов.
Астрономия всегда была близка простым людям, поэтому, возможно, в прошлом она была ближе к человеку, чем сейчас. Мой дед-крестьянин знал то, что сейчас неизвестно большинству городских жителей. К примеру, он рассказывал, что каждую ночь луна восходит на час позже (в действительности на 50 минут, однако подобная точность для крестьянина была несущественной). Моя бабушка знала, что летом солнце стоит выше, чем зимой: его лучи проникали через окно и освещали дальнюю стену комнаты в разное время года по-разному. Интересно, что астрономия больше других наук привлекает любителей во всём мире. Возможно, вызвано это тем, что небо всегда находится у нас над головой, даже в облачный день, а вот, например, любителям-орнитологам надо ехать в какие-то определённые места, что бы наблюдать, как птицы вьют гнёзда. Обилие астрономов-любителей является одной из характерных особенностей данной науки. Благодаря этому распространение новых результатов в астрономии происходит успешно и очень быстро, а некоторым астрономам-любителям удалось добиться больших успехов в изучении небес.
Мне кажется, что распространение результатов астрономических наблюдений происходит проще, чем в других науках, потому что астрономия очень наглядна.
Объяснить последние математические открытия, относящиеся, например, к теории чисел или дифференциальной геометрии, довольно сложно, а продемонстрировать последние снимки, полученные телескопом «Хаббл», нетрудно. Кто из нас, затаив дыхание, не рассматривал фотографии космоса? Более того, астрономия в грамотном изложении по эмоциям и накалу страстей не уступит и сериалу. Кто из нас не удивится, узнав, что звёзды рождаются, стареют и умирают, а некоторые из них ждёт трагическая гибель? Кто не расчувствуется, узнав, что именно внутри звёзд родились самые тяжёлые химические элементы, из которых состоит наше тело? Кто не почувствует себя частью космоса, узнав, что мы — всего лишь дети звёзд, звёздная пыль? Кроме того, во Вселенной движутся и сталкиваются между собой целые галактики. В конечном итоге астрономия — это целый мир, полный прекрасных образов.
Люди хотят узнать об астрономии больше — возможно, потому, что эта наука рассказывает о прошлом, о том, как вращается Земля, о Солнечной системе, о космосе и, следовательно, о нашем доме. И ещё она говорит о том, откуда мы взялись.
Также астрономия позволяет предсказывать смену времён года, затмения, положение планет и звёзд на небе. Этот аспект порой используют псевдоучёные, чтобы предсказать какие-то явления, никак не связанные с расположением небесных тел. Возможно, это является следствием самой природы человека: люди чувствуют неуверенность в будущем и пытаются устранить её любыми способами, например с помощью астрологических прогнозов.
Кстати, если говорить о прогнозах, то между астрономией и математикой существует особая связь, ведь астрономические прогнозы являются результатами математических расчётов. По сути, многие задачи астрономии стало возможным решить благодаря развитию новых разделов математики.
Я ожидаю, что эта книга придётся по душе читателю, и в ней он найдёт ответ на некоторые интересующие его вопросы. Возможно, после чтения у вас возникнут новые идеи — именно таким путём и движется наука. Любой исследователь понимает, что он зажат в рамки: с одной стороны, он испытывает удовольствие от того, что побеждает неподвластную ранее задачу или начинает понимать то, чего раньше не понимал, но, с другой стороны, ему не дают покоя всё новые и новые вопросы.
Я была бы очень рада, если бы читатель получил от этой книги удовольствие сродни исследовательскому. Признаюсь, я работала над ней с наслаждением и надеюсь, что и вы испытаете нечто похожее.
Книга состоит из пяти глав, посвящённых важнейшим темам астрономии, связанным с математикой, — положению планет и измерению времени. В двух первых главах рассказывается об относительном положении небесных тел и расстояниях между ними, в двух последних — об измерении времени. В самой важной, третьей главе, мы поговорим о затмениях — астрономических явлениях, во время которых небесные тела занимают особое положение в пространстве.
Глава 1. Основные углы и расстояния: азбука астрономии
Очевидно, что основной целью науки, посвящённой наблюдению и изучению объектов, является определение их местоположения. В решении этой крайне важной задачи главную роль играет математика, позволяющая вычислить три значения: величины двух углов, указывающих расположение объекта на небесной сфере, и расстояние от объекта до нас. Определить эти два угла сравнительно просто, а вот вычисление расстояний до небесных тел — напротив, одна из сложнейших задач астрономии.
Определение положения по двум углам
Для расчёта положения тела на поверхности Земли используется метод координат. Так как результаты астрономических наблюдений часто зависят от того, где находится наблюдатель, учитывать земные координаты при работе с астрономическими данными крайне важно. Коротко опишем метод расчёта положения небесных тел.
Наша планета вращается вокруг оси, которая обычно используется в качестве линии отсчёта при определении положения точек на поверхности Земли. К примеру, точки пересечения земной оси с поверхностью нашей планеты называются Северным и Южным полюсом. Если мы рассмотрим плоскость, перпендикулярную оси вращения Земли и проходящую через центр нашей планеты, то увидим, что линией пересечения этой плоскости и земной поверхности будет экватор, который делит Землю на два полушария, Северное и Южное (в их вершинах находятся Северный и Южный полюс соответственно). Если теперь мы представим бесконечное число плоскостей, параллельных экватору, и рассечём этими плоскостями поверхность Земли, то получим окружности меньшего размера — параллели.
Теперь представим, что Земля подобна апельсину, разделённому на дольки с помощью линий, проходящих через оба полюса перпендикулярно экватору. Будем называть эти линии меридианами. В отличие от экватора и параллелей, все меридианы имеют равную длину. В 1884 году было принято решение выбрать в качестве нулевого меридиан, проходящий через Гринвичскую обсерваторию близ Лондона. Этот меридиан сохранил свой статус до наших дней, хотя ранее большинство европейских моряков использовали в качестве нулевого меридиан острова Иерро в Канарском архипелаге, точнее меридиан мыса Орчилья на западной оконечности острова. Вызвано это было тем, что со времён Птолемея остров Иерро считался концом известного мира, и до 1492 года о землях, лежащих к западу от острова, ничего не было известно.
Источник
ЕГЭ-2018 по географии: задание 32
Задание 32
(«Земля как планета, современный облик планеты Земля. Форма, размеры, движение Земли»). max 2 балла!
Тип 1. Определите, в каком из обозначенных буквами на карте Северного полушария пунктов, 20 декабря солнце раньше (по времени Гринвичского меридиана) поднимется над горизонтом. Ход ваших рассуждений запишите.
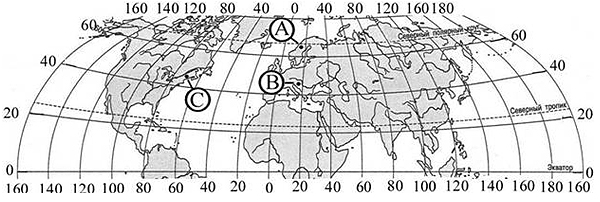
Задание 32 – одно из самых сложных в ЕГЭ по географии. По статистике, его решают менее 30% сдававших экзамен. В то же время, оно не так трудно, как кажется на первый взгляд, если точно придерживаться алгоритма его решения.
В первом из типов задания 32 необходимо найти точку, в которой солнце раньше (или позже) всего поднимется над горизонтом. Это зависит от двух факторов:
1. Долготы точки. Солнце встаёт на востоке, следовательно, чем восточнее расположена точка, тем раньше солнце будет подниматься в ней над горизонтом.
2. Широты точки. Здесь важно время года.
Летом северного полушария (с 21 марта по 23 сентября) продолжительность дня будет возрастать от Южного полюса к Северному, следовательно, чем дальше на север будет расположена точка, тем раньше там будет всходить солнце.
Зимой же всё меняется с точностью до наоборот. Продолжительность дня будет возрастать при движении на юг, следовательно, чем южнее расположена точка, тем раньше там будет всходить солнце.
В приведённом задании точки А и В расположены восточнее точки С, следовательно, в точке С солнце взойдёт позже. Так как точки А и В лежат на одном меридиане, то время восхода солнца будет зависеть от продолжительности светового дня в них. 20 декабря день будет длиннее в точке В, т.к. она лежит южнее точки А.
Следовательно, солнце раньше поднимется над горизонтом в точке B.
Алгоритм 1
(при поиске точки, где солнце взойдёт раньше всего):
- Выбираем точку(и), лежащую(ие) восточнее всего.
- Если на одном меридиане располагаются две точки, то выбираем ту, в которой продолжительность дня в данное время года больше.
Эмпирическая подсказка: примерно в 85% случаев искомая точка располагается «в вершине» угла, образуемого тремя точками. Т.е. на одной параллели с одной из точек и на одном из меридианов с другой.
Тип 2. Определите, в какой из точек, географические координаты которых указаны в таблице, 18 марта Солнце будет находиться выше всего над горизонтом в 15 часов по солнечному времени гринвичского меридиана. Запишите обоснование Вашего ответа.
Во втором типе задания 32 требуется найти точку, в которой солнце расположено выше всего над горизонтом. Что характерно, это также зависит от двух факторов:
1. Широты точки. Чем ближе к экватору расположена точка, тем выше в ней стоит солнце над горизонтом*.
2. Долготы точки. Чем ближе к полуденному меридиану находится точка, тем выше в ней стоит солнце над горизонтом.
Таким образом, основная сложность при выполнении этого типа задания связана с нахождением полуденного меридиана – меридиана, на котором в данный момент времени полдень. Т.к. окружность Земли составляет 360°, а в сутках 24 часа, то за один час Земля поворачивается на 360 : 24 = 15°. Следовательно, чтобы найти полуденный меридиан, нужно разницу во времени нулевого и полуденного меридиана умножить на 15°.
В приведённом задании на Гринвиче 15 часов, следовательно, разница со временем полуденного меридиана составляет 3 часа (15 – 12), а градусная мера последнего составит (15 – 12) · 15° = 45° з.д. Долгота западная потому, что полуденный меридиан лежит к западу от Гринвича (там уже три часа дня, а солнце движется с востока на запад)**.
Точки А и Б лежат ближе к полуденному меридиану, чем точка В. При этом точка А расположена ближе к экватору, следовательно, именно там солнце и будет располагаться выше всего над горизонтом.
Алгоритм 2
(при поиске точки, в которой солнце стоит выше всего над горизонтом):
- Находим точку(и), расположенную(ые) ближе всего к полуденному меридиану. Долготу полуденного меридиана рассчитываем по формуле λ = (t – 12) · 15°, где λ – долгота, t – время гринвичского меридиана. Если число отрицательное, то долгота восточная.
- Если на одном меридиане располагаются две точки, то выбираем ту, которая расположена ближе к экватору.
Эмпирическая подсказка: если вы лучше воспринимаете информацию в графическом виде, нежели чем в табличном, то нарисуйте схематически на черновике две параллели и два меридиана и расположите на их пересечениях указанные точки.
* Из этого правила есть исключения, когда точка расположена между тропиками, но такие точки практически не попадаются в заданиях ЕГЭ.
** А ёщё можно посмотреть на долготу данных точек – в 90% случаев полушария совпадают.
Тип 3. Определите географические координаты пункта, расположенного в США, если известно, что 23 сентября в 17 часов по солнечному времени Гринвичского меридиана в этом пункте полдень и солнце находится на высоте 53° над горизонтом. Ход ваших рассуждений запишите.
Этот тип задания 32 требует исключительно математических расчётов.
Для нахождения широты точки воспользуемся известной нам высотой солнца над горизонтом (он же – угол падения солнечных лучей) в полдень. В дни равноденствий* солнечные лучи падают отвесно (под 90°) на экваторе, т.е. на 0° широты. А на полюсах (90° широты) солнце находится точно на горизонте, т.е. угол падения лучей равен 0°.
Следовательно, между географической широтой и углом падения солнечных лучей наблюдается обратная зависимость, которую можно выразить формулой φ = 90°– α, где φ – широта точки, α – угол падения солнечных лучей в полдень в дни равноденствия.
Чтобы найти долготу точки, нам потребуется выполнить вычисления, аналогичные таковым для типа 2, т.е. найти полуденный меридиан, градусная мера которого и будет долготой искомой точки, по формуле λ = (t – 12) · 15°, где λ – долгота точки, t – время гринвичского меридиана.
В данном задании широта составит φ = 90° – 53° = 37° с.ш. Широта северная только потому, что точка, как мы помним, расположена на территории США.
Долгота точки будет равна λ = (17 – 12) · 15° = 75° з.д., долгота западная потому, что время в данной точке отстаёт от Гринвича.
Алгоритм 3
(при поиске координат точки, для которой известна высота полуденного солнца и разница во времени с Гринвичем):
- Находим широту точки, используя формулу φ = 90° – α, где φ – широта точки, α – угол падения солнечных лучей в полдень в дни равноденствия.
- Находим долготу точки по формуле λ = (t – 12) · 15°, где λ – долгота точки, t – время гринвичского меридиана. Если число отрицательное, то долгота восточная.
- Записываем полученные координаты с указанием значения широты и долготы.
* В этом типе заданий дело происходит либо 23 сентября, либо 21 марта, т.е. в дни равноденствий.
Источник







