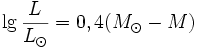Звёздная величина (из Википедии)
Звёздная величина — числовая характеристика объекта на небе, чаще всего звезды, показывающая, сколько света приходит от него в точку, где находится наблюдатель.
Современное понятие видимой звёздной величины сделано таким, чтобы оно соответствовало величинам, приписанным звёздам древнегреческим астрономом Гиппархом во II веке до н. э. Гиппарх разделил все звёзды на шесть величин. Самые яркие он назвал звёздами первой величины, самые тусклые — звёздами шестой величины. Промежуточные величины он распределил равномерно между оставшимися звёздами.
Видимая звёздная величина зависит не только от того, сколько света излучает объект, но и от того, на каком расстоянии от наблюдателя он находится. Видимая звёздная величина считается единицей измерения блеска звезды, причём чем блеск больше, тем величина меньше, и наоборот.
В 1856 году Н. Погсон предложил формализацию шкалы звёздных величин. Видимая звёздная величина определяется по формуле:

Поскольку данная шкала относительная, то её нуль-пункт (0 m ) определяют как яркость такой звезды, у которой световой поток равен 10³ квантов /(см²·с·Å) в зелёном свете (шкала UBV) или 10 6 квантов /(см²·с·Å) во всём видимом диапазоне света. Звезда 0 m за пределами земной атмосферы создаёт освещённость в 2,54·10 −6 люкс.
Шкала звёздных величин является логарифмической, поскольку изменение яркости в одинаковое число раз воспринимается как одинаковое (закон Вебера — Фехнера). Кроме того, поскольку Гиппарх решил, что величина тем меньше, чем звезда ярче, то в формуле присутствует знак минус.
Следующие два свойства помогают пользоваться видимыми звёздными величинами на практике:
- Увеличению светового потока в 100 раз соответствует уменьшение видимой звёздной величины ровно на 5 единиц.
- Уменьшение звёздной величины на одну единицу означает увеличение светового потока в 10 1/2,5 =2,512 раза.
В наши дни видимая звёздная величина используется не только для звёзд, но и для других объектов, например, для Луны и Солнца и планет. Поскольку они могут быть ярче самой яркой звезды, то у них может быть отрицательная видимая звёздная величина.
Видимая звёздная величина зависит от спектральной чувствительности приёмника излучения (глаза, фотоэлектрического детектора, фотопластинки и т. п.)
- Визуальная звёздная величина (V или mv ) определяется спектром чувствительности человеческого глаза (видимый свет), имеющего максимум чувствительности при длине волны 555 нм. или фотографически с оранжевым фильтром.
- Фотографическая или «синяя» звёздная величина (B или mp ) определяется фотометрированием изображения звезды на фотопластинке, чувствительной к синим и ультрафиолетовым лучам, или при помощи сурьмяно-цезиевого фотоумножителя с синим фильтром.
- Ультрафиолетовая звёздная величина (U) имеет максимум в ультрафиолете при длине волны около 350 нм.
Разности звёздных величин одного объекта в разных диапазонах U−B и B−V являются интегральными показателями цвета объекта, чем они больше, тем более красным является объект.
- Болометрическая звёздная величина соответствует полной мощности излучения звезды, т. е. мощности, просуммированной по всему спектру излучения. Для её измерения применяется специальное устройство — болометр.
абсолютная
Абсолютная звёздная величина (M) определяется как видимая звёздная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя. Абсолютная болометрическая звёздная величина Солнца +4,7. Если известна видимая звёздная величина и расстояние до объекта, можно вычислить абсолютную звёздную величину по формуле:

Соответственно, если известны видимая и абсолютная звёздные величины, можно вычислить расстояние по формуле
Абсолютная звёздная величина связана со светимостью следующим соотношением: 


Звёздные величины некоторых объектов
| Объект | m |
| Солнце | −26,7 |
| Луна в полнолуние | −12,7 |
| Вспышка Иридиума (максимум) | −9,5 |
| Сверхновая 1054 года (максимум) | −6,0 |
| Венера (максимум) | −4,4 |
| Земля (глядя с Солнца) | −3,84 |
| Марс (максимум) | −3,0 |
| Юпитер (максимум) | −2,8 |
| Международная космическая станция (максимум) | −2 |
| Меркурий (максимум) | −1,9 |
| Галактика Андромеды | +3,4 |
| Проксима Центавра | +11,1 |
| Самый яркий квазар | +12,6 |
| Самые слабые звёзды, наблюдаемые невооружённым глазом | От +6 до +7 |
| Самый слабый объект, заснятый в 8-метровый наземный телескоп | +27 |
| Самый слабый объект, заснятый в космический телескоп Хаббла | +30 |
| Объект | Созвездие | m |
| Сириус | Большой пёс | −1,47 |
| Канопус | Киль | −0,72 |
| α Центавра | Центавр | −0,27 |
| Арктур | Волопас | −0,04 |
| Вега | Лира | 0,03 |
| Капелла | Возничий | +0,08 |
| Ригель | Орион | +0,12 |
| Процион | Малый пёс | +0,38 |
| Ахернар | Эридан | +0,46 |
| Бетельгейзе | Орион | +0,50 |
| Альтаир | Орёл | +0,75 |
| Альдебаран | Телец | +0,85 |
| Антарес | Скорпион | +1,09 |
| Поллукс | Близнецы | +1,15 |
| Фомальгаут | Южная рыба | +1,16 |
| Денеб | Лебедь | +1,25 |
| Регул | Лев | +1,35 |
Солнце с разных расстояний
Источник
Звёздная величина
Звёздная величина (блеск) — безразмерная числовая характеристика яркости объекта, обозначаемая буквой m . Обычно понятие применяется к небесным светилам. Звёздная величина характеризует поток энергии от рассматриваемого светила (энергию всех фотонов в секунду) на единицу площади. Таким образом, видимая звёздная величина зависит и от физических характеристик самого объекта (то есть светимости), и от расстояния до него. Чем меньше значение звёздной величины, тем ярче данный объект. Понятие звёздной величины используется при измерении потока энергии в видимом, инфракрасном и ультрафиолетовом диапазоне. В звёздных величинах измеряется проницающая сила телескопов и астрографов.
Ещё во II веке до н. э. древнегреческий астроном Гиппарх разделил все звёзды на шесть величин. Самые яркие он назвал звёздами первой величины, самые тусклые — звёздами шестой величины, а остальные равномерно распределил по промежуточным величинам.
Как выяснилось позже, связь такой шкалы с реальными физическими величинами логарифмическая, поскольку изменение яркости в одинаковое число развоспринимается глазом как изменение на одинаковую величину (закон Вебера — Фехнера). Поэтому в 1856 году Норман Погсон предложил следующую формализацию шкалы звёздных величин, ставшую общепринятой:
где m — звёздные величины объектов, L — освещённости от объектов. Такое определение соответствует падению светового потока в 100 раз при увеличении звёздной величины на 5 единиц.
Данная формула даёт возможность определить только разницу звёздных величин, но не сами величины. Чтобы с её помощью построить абсолютную шкалу, необходимо задать нуль-пункт — блеск, которому соответствует нулевая звездная величина (0 m ). Сначала в качестве 0 m был принят блеск Веги. Потом нуль-пункт был переопределён, но для визуальных наблюдений Вега до сих пор может служить эталоном нулевой видимой звёздной величины (по современной системе, в полосе V системы UBV её блеск равен +0,03 m , что на глаз неотличимо от нуля).
По современным измерениям, звезда нулевой видимой величины за пределами земной атмосферы создаёт освещённость в 2,54 × 10 −6 люкс. Световой поток от такой звезды примерно равен 10 3 квантов/(см²·с·Å) в зелёном свете (полоса V системы UBV) или 10 6 квантов/(см²·с) во всём видимом диапазоне света.
Следующие свойства помогают пользоваться видимыми звёздными величинами на практике:
· Увеличению светового потока в 100 раз соответствует уменьшение видимой звёздной величины ровно на 5 единиц.
· Уменьшение звёздной величины на одну единицу означает увеличение светового потока в 100 1/5 ≈ 2,512 раза.
В наши дни понятие звёздной величины используется не только для звёзд, но и для других объектов, например, для Луны и планет. Звёздная величина самых ярких объектов отрицательна. Например, блеск Луны в полной фазе достигает −12,7 m , а блеск Солнца равен −26,7 m .
Видимая и абсолютная звёздная величина
Широко используется понятие абсолютной звёздной величины (M). Это звёздная величина объекта, которую он имел бы, если бы был на расстоянии 10 парсек от наблюдателя. Абсолютная величина, в отличие от видимой, позволяет сравнивать светимость разных звёзд, поскольку не зависит от расстояния до них.
Наблюдающаяся с Земли звёздная величина называется видимой (m). Это название используется, чтобы отличать её от абсолютной, и применяется даже для величин, измеренных в ультрафиолетовом, инфракрасном или каком-либо другом не воспринимаемом глазом диапазоне излучения (величина, измеренная в видимом диапазоне, называется визуальной). Абсолютная болометрическая звёздная величина Солнца равна +4,8 m , а видимая составляет −26,7 m .
Звёздная величина зависит от спектральной чувствительности приёмника излучения (глаза, фотоэлектрического детектора, фотопластинки и т. п.)
· Болометрическая звёздная величина показывает полную мощность излучения звезды (то есть мощность излучения на всех длинах волн). Для её измерения применяется специальное устройство — болометр. Актуальность этой величины связана с тем, что некоторые звёзды (очень горячие и очень холодные) излучают преимущественно не в видимом спектре.
Однако чаще всего звёздные величины измеряют в определённых интервалах длин волн. Для этого разработаны фотометрические системы, в каждой из которых есть набор полос, перекрывающих разные диапазоны волн. В пределах каждой полосы чувствительность максимальна для некоторой длины волны и плавно спадает с удалением от неё.
Самой распространённой фотометрической системой является система UBV, которая состоит из трёх полос, перекрывающих разные интервалы длин волн. В ней для каждого объекта можно измерить 3 звёздные величины:
· Визуальная звёздная величина (V) — звёздная величина в фильтре V, максимум пропускания которого близок к максимуму чувствительности человеческого глаза (555 нм).
· «Синяя» звёздная величина (B) характеризует яркость объекта в синей области спектра; максимум чувствительности на длине волны около 445 нм.
· Ультрафиолетовая звёздная величина (U) имеет максимум в ультрафиолетовой области при длине волны около 350 нм.
Разности звёздных величин одного объекта в разных диапазонах (для системы UBV это U−B и B−V) являются показателями цвета объекта: чем они больше, тем более красным является объект. Фотометрическая система UBV определена таким образом, чтобы показатели цвета звёзд спектрального класса А0V равнялись нулю.
Существуют и другие фотометрические системы, в каждой из которых может быть определён свой набор звёздных величин.
· Фотографическая звёздная величина — определяется для спектральной чувствительности несенсибилизированной фотоэмульсии с максимумом чувствительности на длине волны 425 нм; по определению совпадает с визуальной звёздной величиной для звёзд А0V и блеском (6,0±0,5) m . Вместе с фотовизуальной звёздной величиной использовалась в устаревшей фотографической системе звёздных величин.
Звёздные величины некоторых объектов
Источник
Звездная величина солнца таблица
В астрономии, говоря о небесных телах, иногда используются специфические термины, характеризующие их цвет и яркость, например, звездная величина или показатель цвета.
Мы можем также определить отношение, оперируя понятиями коэффициента яркости:
При этом пока все еще не так просто. Звезда или иной объект излучает (или отражает) свет разных длин волн — а человек их воспринимает по-разному. При одной и той же интенсивности зеленый свет воспринимается ярче, красный — тусклее, а инфракрасный, разумеется, не воспринимается вовсе.
Абсолютные звёздные величины
Видимый блеск и видимая звёздная величина звезды зависят от её расстояния до наблюдателя – r. Чтобы освободиться от влияния расстояния, введено понятие об абсолютном блеске и абсолютной величине звезды .
Абсолютным блеском звезды L называется тот блеск, который она имела бы, будучи удалена от наблюдателя на расстояние равное 10 парсекам.
Так как освещённость убывает обратно пропорционально квадрату расстояния, то абсолютный блеск L и видимый блеск l связаны соотношением:
L/l = r 2 /100 = 2,512 m-M
m – видимая звёздная величина, М – абсолютная звёздная величина, под которой понимают ту звёздную величину, которую бы имела звезда, будучи удалённой на расстояние, равное 10 парсекам.
Из указанного соотношения получаем формулу:
М = m + 5 — 5lg r
С учётом межзвёздного поглощения:
М = m + 5 — 5lg r — А(r)
где А(r) – поглощение света, пропорциональное расстоянию до звезды.
Эта формула позволяет вычислить абсолютную звёздную величину звезды, если известно расстояние, и вычислить расстояние, если известна абсолютная величина, по формуле:
lg r = (m — M)/5 + 1
Абсолютные звёздные величины могут быть болометрическими, визуальными, фотографическими.
Солнце имеет абсолютную звёздную величину +4,7 m .
Часто используют светимость звезды – отношение абсолютного блеска звезды к абсолютному блеску Солнца.
Самые яркие звёзды ярче Солнца на 14 m , они испускают больше энергии в 1 000 000 раз. Самые слабые слабее на 14 m . Они испускают меньше энергии в 300 000 раз.
Отношение светимостей самых ярких и самых слабых звёзд достигает около 100 млрд.
Светимость (блеск) звезд
Представьте, что где-то в море в ночной тьме тихо мерцает огонек. Если бывалый моряк не объяснит вам, что это, вы часто и не узнаете: то ли перед вами фонарик на носу проходящей шлюпки, то ли мощный прожектор далекого маяка.
В том же положении в темную ночь находимся и мы, глядя на мерцающие звезды. Их видимый блеск зависит и от их истинной силы света, называемой светимостью (полное количествл энергии, излучаемой по всем направлениям), и от их расстояния до нас. Только знание расстояния до звезды позволяет подсчитать ее светимость по сравнению с Солнцем. Так например, светимость звезды, в десять раз менее яркой в действительности, чем Солнце, выразится числом 0,1.
Истинную силу света звезды можно выразить еще иначе, вычислив, какой звездной величины она бы нам казалась, если бы она находилась от нас на стандартном расстоянии в 32,6 светового года, то есть на таком, что свет, несущийся со скоростью 300 000 км/сек, прошел бы его за это время.
где R — радиус звезды, Т — температура.
Принять такое стандартное расстояние оказалось удобным для различных расчетов. Яркость звезды, как и всякого источника света, изменяется обратно пропорционально квадрату расстояния от него. Этот закон позволяет вычислять абсолютные звездные величины или светимости звезд, зная расстояние до них.
Когда расстояния до звезд стали известны, то мы смогли вычислить их светимости, то есть смогли как бы выстроить их в одну шеренгу и сравнивать друг с другом в одинаковых условиях. Надо сознаться, что результаты оказались поразительными, поскольку раньше предполагали, что все звезды «похожи на наше Солнце». Светимости звезд оказались поразительно разнообразными, и их в нашей шеренге не сравнить ни с какой шеренгой пионеров.
Приведем только крайние примеры светимости в мире звезд.
Самой слабой из известных долго являлась звезда, которая в 50 тысяч раз слабее Солнца, и ее абсолютная величина светимости: +16,6. Однако, впоследствии были открыты и ещё более слабые звезды, светимость которых, по сравнению с солнцем, меньше в миллионы раз!
Размеры в космосе обманчивы: Денеб с Земли сияет ярче Антареса, а вот Пистолет — не виден совсем. Тем не менее, наблюдателю с нашей планеты и Денеб и Антарес кажутся просто незначительными точками, по сравнению с Солнцем. Насколько это неверно можно судить по простому факту: Пистолет выпускает в секунду столько же света, сколько Солнце — за год!
На другом краю шеренги звезд стоит «S» Золотой Рыбы, видимая только в странах Южного полушария Земли как звездочка восьмой величины (то есть даже не видимая без телескопа!). В действительности она в 400 тысяч раз ярче Солнца, и ее абсолютная величина светимости: —8,9.
Абсолютная величина светимости нашего Солнца равна +5. Не так уж и много! С расстояния в 32,6 светового года мы бы его плохо видели без бинокля.
Если яркость обычной свечи принять за яркость Солнца, то в сравнении с ней «S» Золотой Рыбы будет мощным прожектором, а самая слабая звезда слабее самого жалкого светлячка.
Итак, звезды — это далекие солнца, но их сила света может быть совершенно иной, чем у нашего светила. Образно выражаясь, менять наше Солнце на другое нужно было бы с оглядкой. От света одного мы ослепли бы, при свете другого бродили бы, как в сумерках.
Источник